A small ball A is.thrown up with a velocity 40ms from the ground. Another identical ball B of same mass is just dropped from a height of 50m simultaneously at time t=0 so that both collide in air and stick together. Find the value of t (in s) at which combined mass will fall to the ground. (g=10m(s)2)
'(##CEN_KSR_PHY_JEE_C08_E01_023_Q15##)'
The correct Answer is:5
Topper's Solved these Questions
Similar Questions
A sphere A is thrown up with velocity 20m/sec from the ground. Sphere B of same mass is dropped from a height of 80 m simultaneously, at time t = 0 so that both collide in air and stick together. Find the time (in second) after which the combined mass will fall on the ground. (Calculate from t = 0)(g=10m/sec2)
View SolutionA sphere A is thrown up with velocity 20m/sec from the ground. Sphere B of same mass is dropped from a height of 80 m simultaneously, at time t = 0 so that both collide in air and stick together. Find the time (in second) after which the combined mass will fall on the ground. (Calculate from t = 0)(g=10m/sec2)

View Solution
Knowledge Check
A ball is thrown from the ground with a velocity of 20√3 m/s making an angle of 60∘ with the horizontal. The ball will be at a height of 40 m from the ground after a time t equal to (g=10ms−2)
A√2 secB√3 secC2 secD3 sec
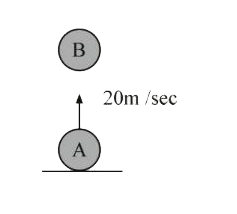
Two identiacal masses are as shown in figure. One is thrown upwards with velocity 20 m/s and another is just dropped simultaneously.
The masses collide I air and stick together. After how much time the combined mass will fall to the gorund (calculate the time from the starting when the motion was started )
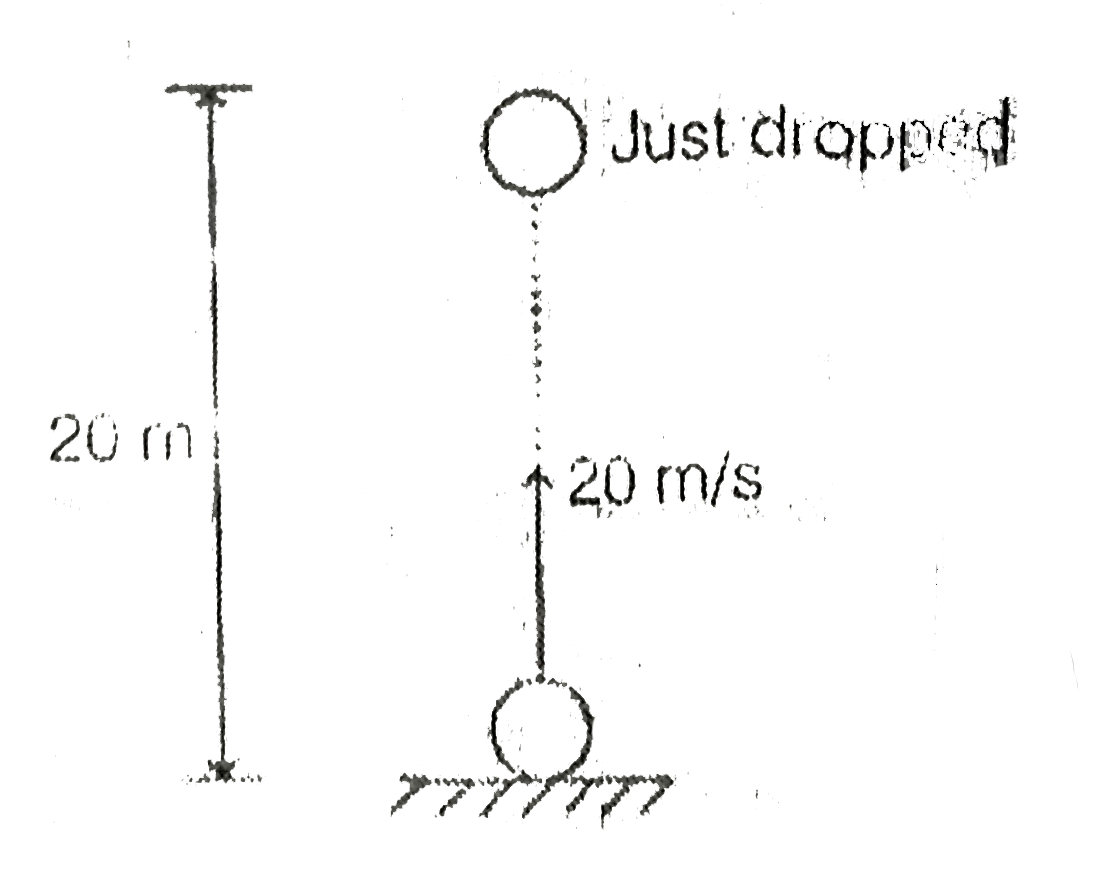
View SolutionTwo identiacal masses are as shown in figure. One is thrown upwards with velocity 20 m/s and another is just dropped simultaneously.
The masses collide I air and stick together. After how much time the combined mass will fall to the gorund (calculate the time from the starting when the motion was started )
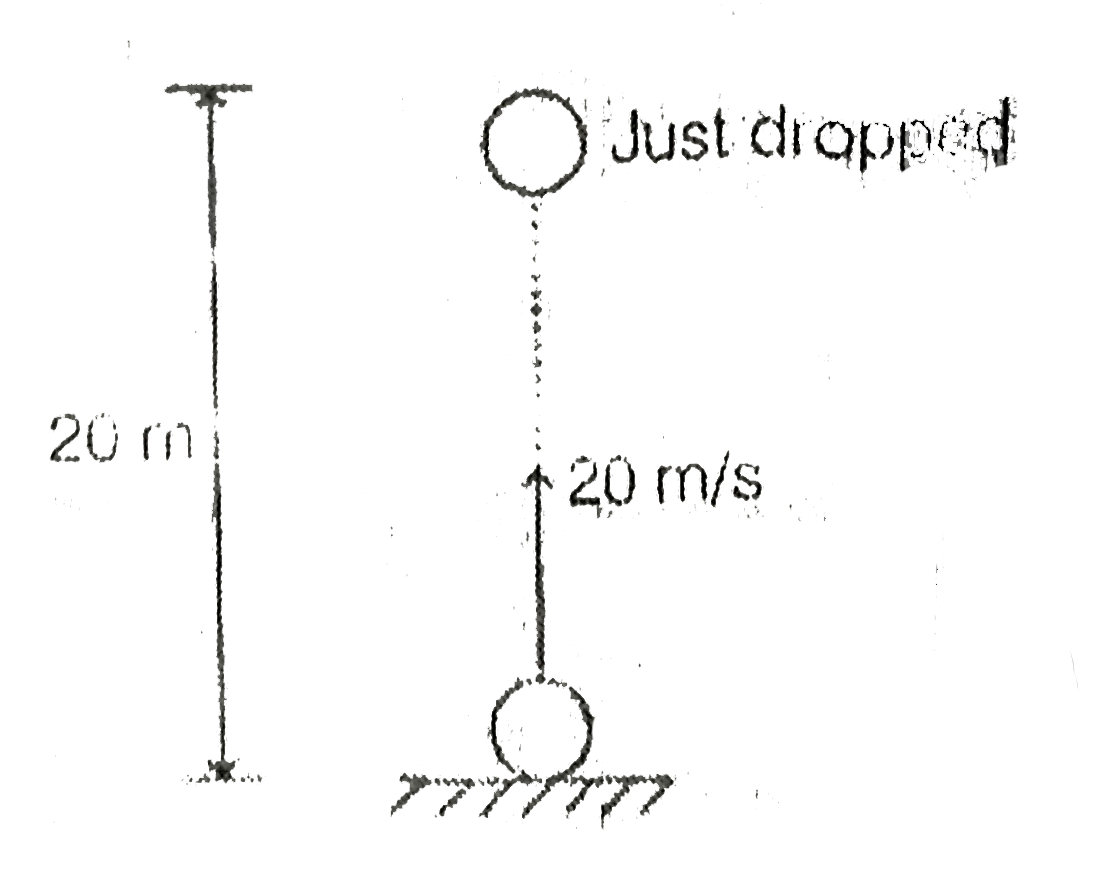
View SolutionA ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. The relative speed of the balls varies with time as
View SolutionA balloon is ringing up with constant velocity of 10 m/s. At a height of 75m a small mass is dropped from it. At what height from the ground would the balloon be when the mass reaches the ground?
View SolutionA ball 'A' is thrown upwards from ground level with a velocity of 20ms−1. Another ball 'B' is thrown downwards from a height of 40 m with the same speed. Find the height at which the two balls meet (take g=10ms−2).
View SolutionA ball is dropped from a balloon rising up with a velocity of 50 m/s. When the ball is dropped the balloon was at a height of 100 m. Find the time taken by the ball to reach the ground.
View SolutionA ball is thrown from the top of a building with a velocity of 10 m/s and returns with a velocity of 30 m/s to the ground. Find the height of the building.
View Solution

