Suppose f(x)=ax+b and g(x)=bx+a, where a and b are positive integers. If f(g(50))−g(f(50))=28 then find the sum of all possible values of a is equal to
The correct Answer is:21
Topper's Solved these Questions
- FUNCTIONSBOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- EQUATION OF PLANE AND ITS APPLICATIONS -IIBOOK - CENGAGECHAPTER - EQUATION OF PLANE AND ITS APPLICATIONS -IIEXERCISE - DPP 3.4
19 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
Similar Questions
Let f(x)=x2−2x−1∀ξnR Let f:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective. If f:R→R , g(x)=f(x)+3x−1 , then the least value of function y=g(|x|) is
View SolutionLet A(0,6,6), B(6,6,0) and C(6,0,6) are three points and point D is moving on the line x+z−3=0=y. If G is centroid of ΔABC, then minimum value of GD is
View SolutionDoes the following graph pass the vertical or horizontal line test ?
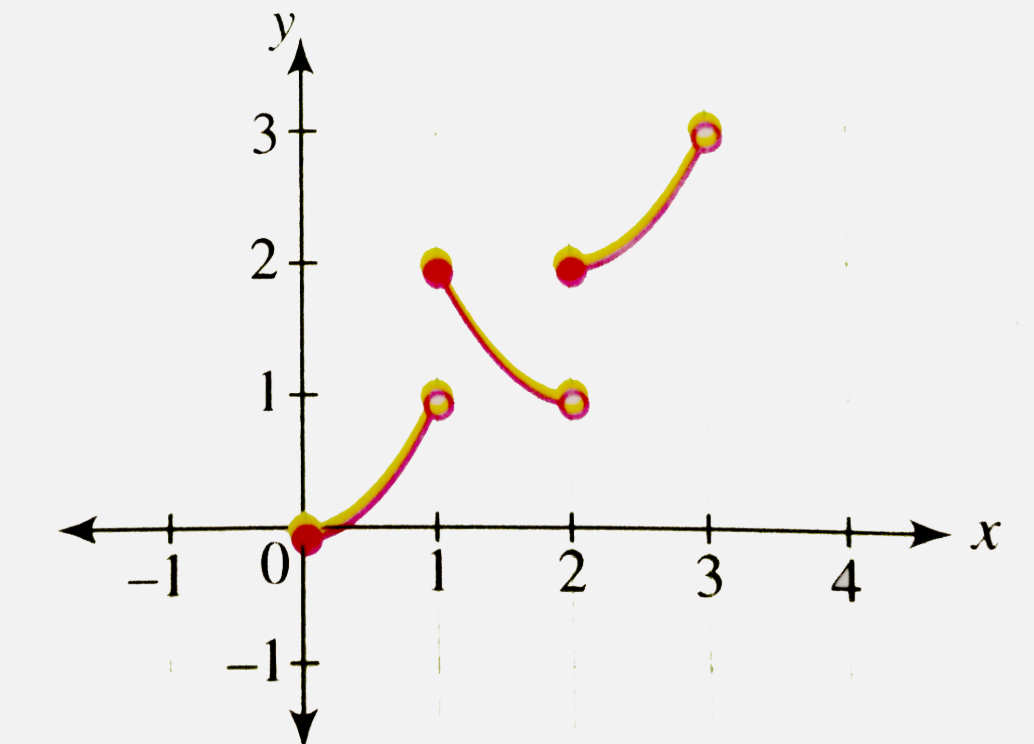
View SolutionIf f(x)=(ax2+b)3, then find the function g such that f(g(x))=g(f(x)).
View Solutionif (d)/(dx)f(x)=g(x), find the value of int_(a)^(b)f(x)g(x)dx
View SolutionSuppose f(x)-ax+b and g(x)=bx+a where a and b are positive integets If f(g(50))-g(f(50))=28 then the product (ab) can have the value equal to
View SolutionIf the functions f(x) and g(x) are continuous on [a,b] and differentiable on (a,b) then in the interval (a,b) the equation
∣∣∣f'(x)f(a)g'(x)g(a)∣∣∣=1a−b=∣∣∣f(a)f(b)g(a)g(b)∣∣∣
View SolutionIf f and g are derivable function of x such that g'(a)≠0,g(a)=b and f(g(x))=x,then'f'(b)=
View Solutionf and g differentiable functions of x such that f(g(x))=x, If g'(a)≠0 and g(a)=b, then f'(b)=
View SolutionIf f(x+y)=f(x)f(y) and f(x)=1+xg(x) G(x), where limx→0g(x)=a and limx→0G(x)=b. Then f'(x) is equal to :
View SolutionSuppose f(x)=ax+bandg(x)=bx+a,whereaandb are positive integers. If f(g(50))−g(f(50))=28, then the product (ab) can have the value equal to
View SolutionSuppose f and g are functions having second derivatives f'andg' every where, if f(x).g(x)=1 for all xandf'',g'' are never zero then f''(x)f'(x)−g''(x)g'(x) equals
View SolutionSuppose f and g are functions having second derivatives f'' and g'' every where . If f(x) .g(x) = 1 for all x and f' and g' are never zero then f''(x)f'(x)−g''(x)g'(x) equals
View SolutionIf f(x)=(ax2+b)3, then find the function g such that f(g(x))=g(f(x)).
View SolutionIf the functions f(x) and g(x) are continuous on [a,b] and differentiable on (a,b) then in the interval (a,b) the equation
∣∣∣f'(x)f(a)g'(x)g(a)∣∣∣=1a−b=∣∣∣f(a)f(b)g(a)g(b)∣∣∣
View Solution

