If A=[2513],B=[4−2−13] and I is the identify matric of the same order and At is the transpose of matrix A, find AtB+BI.
The correct Answer is:=[11−3162]
Step by step video & text solution for If A=[{:(,2,5),(,1,3):}], B=[{:(,4,-2),(,-1,3):}] and I is the identify matric of the same order and A^(t) is the transpose of matrix A, find A^(t) B+BI. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A manufacturer sells a washing machine to a wholsaler for Rs 15,000. The wholsaler sells it to a trader at a profit of Rs 1,200 and the trader in turn sells it to a consumer at a profit of Rs 1,800. If the rate of VAT is 8% find,
(i) The amount of VAT received by the State Government on the sale of this machine from the manufacturer and the wholsaler.
(ii) The amount that the consumer pays for the machine.
View SolutionUse a graph paper for this question take 1 cm = 1 unit along both the X and Y axis :
(i) Plot the points A(0, 5), B(2, 5), C(5, 2), D(5, -2), E(2, -5) and F(0, -5).
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
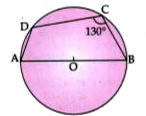
∠BCD=130∘. Find
(i) ∠DAB
View Solutionif A=[[1,3,-40,2,1]] then find out transpose of matrix A.
View SolutionIf A+B^T=[(1,3),(4,5)] and A^T-B=[(7,8),(-1,3)] , then find matrices A and B.
View Solutionfind the transpose of the matrix A=[13−4021].
View SolutionIf A=[[2,5],[1,3]],B=[[4,-2],[-1,3]] and I is the identity matrix of the same order and A^T is transpose of matrix A then find A^(T)B+BI
View SolutionIf A=[125−13−4]andB=⎡⎢⎣3−210−1452−1⎤⎥⎦, show that,
(AB)T=BTAT where AT is the transpose of A.
View SolutionLet A and B be two matrices such that the order of A is 5×7. If ATB and BAT are both defined, then (where AT is the transpose of matrix A)
View SolutionIf A and B are matrices of the same order, then ABT−BTA is a (a) skew-symmetric matrix (b) null matrix (c) unit matrix (d) symmetric matrix
View SolutionIf A and B are matrices of the same order, then ABT−BAT is a (a) skew-symmetric matrix (b) null matrix (c) unit matrix (d) symmetric matrix
View SolutionFind the matrix B such that [4332] B=[2513]
View SolutionIf matrix A=[2134−32]andB=[3−274], find transpose matrices AtandBt. If possible, find (i) A+At (ii) B+Bt
View SolutionIf A=[2513],B=[4−2−13] and I is the identify matric of the same order and At is the transpose of matrix A, find AtB+BI.
View Solutionfind the transpose of the matrix A=[13−4021].
View SolutionLet A and B be two matrices such that the order of A is 5×7. If ATB and BAT are both defined, then (where AT is the transpose of matrix A)
View Solution