Represent the complex numbers
1+7i(2−i)2 in polar form
√2(cos(3pi)/4-isin3π4)
√2(cos(3pi)/4+isin3π4)
√2(cos(7pi)/4+isin7π4)
√2(cos(7pi)/4-isin7π4)
The correct Answer is:B
Step by step video solution for Represent the complex numbers (1+7i)/((2-i)^(2)) in polar form by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:AAKASH INSTITUTE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:Assignment (Section -C) (objective Type Questions ( more thena one options are correct )
Explore 35 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:AAKASH INSTITUTE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:Assignment (Section -D) Linked comprehension Type Questions
Explore 14 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:AAKASH INSTITUTE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:Assignment (Section -A) (objective Type Questions ( one option is correct)
Explore 47 Videos
- BINOMIAL THEOREMBook:AAKASH INSTITUTE ENGLISHChapter:BINOMIAL THEOREMExercise:Assignment (section-J) Objective type question (Aakash Challengers Questions)
Explore 4 Videos
- CONIC SECTIONSBook:AAKASH INSTITUTE ENGLISHChapter:CONIC SECTIONSExercise:SECTION - J ( Aakash Challengers Questions )
Explore 16 Videos
Similar Questions
If |3z-1|=3|z-2|, then z lies on
View SolutionLet z1,α,β be complex numbers of which αandβ constants and z1 varies. If z2 is given in terms of z1 by one of the following equations, it is required to find z2 corresponding to z1 then
In the given figure
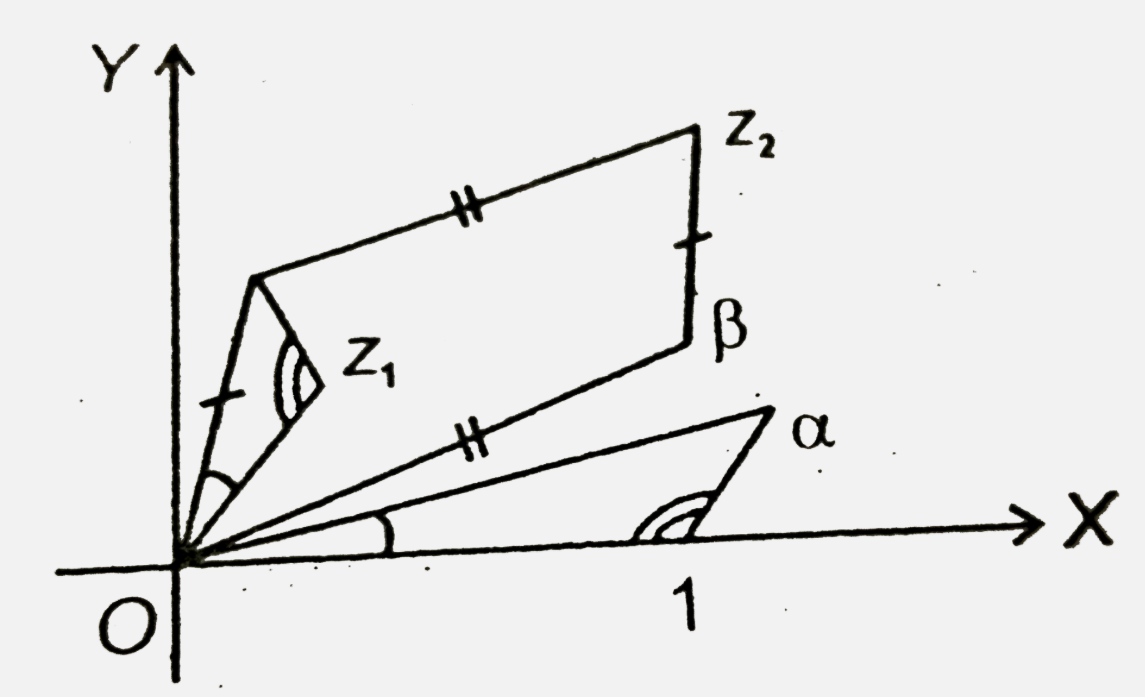
View SolutionThe value of i−9999 is
View SolutionFor any natural number n, the number A given by A=2903n−803n−464n+261n is divisible by
View SolutionFind the angle between the two tangents from the origin to the circle (x−7)2+(y+1)2=25
View SolutionExpress the following complex number in the polar form: (i) (1+7i)/((2-i)^(2))( ii) (1+3i)/(1-2i)
View Solutionनिम्नलिखित संख्याओं को ध्रुवीय रूप (polar form) में निरूपित कीजिए ।
(i) 1+7i(2−i)2 (ii) 1+2i1−3i
View SolutionIf Z=1+7i(2−i)2then the polar form of z is
View SolutionRepresent the complex numbers
−1+i and (−√3−i) in polar form.
View SolutionConvert the following in the polar form:
1+7i(2−i)2
View SolutionRepresent the complex number √3+i in the polar form.
View SolutionConvert the following in the polar form: 1+7i(2−i)2
View Solutionसम्मिश्र संख्या Z=1+7i(2−i)2 का ध्रुवीय रूप है -
View SolutionRepresent the complex numbers
1+7i(2−i)2 in polar form
View SolutionChange the following complex numbers into polar form
1+7i(2−i)2
View Solutionਹੇਠਾਂ ਦਿੱਤੇ ਨੂੰ ਧਰੁਵੀ ਰੂਪ ਵਿੱਚ ਬਦਲੋ:- 1+7i(2−i)2
View Solution
