Two clocks A and B being tested against a standard clock located in the national laboratory At 10.00 AM by the standard clock, the readings of the two clocks are shown in following table
DayClock AClock BIst10:00:068:15:00IInd10:01:138:15:0.1IIIrd9:59:0.88:15:04IVth10:02:158:14:58Vth9:58:108:15:02
If you are doing an experiment that requires precision time interval measurements, which of the two clocks will you prefer ?
The correct Answer is:Clock 2
To determine which clock, A or B, is preferable for precision time interval measurements, we need to analyze the readings of both clocks over the five time points provided. Precision in measurements refers to how closely the measurements are grouped together, regardless of their accuracy.
1. List the Readings:
- Clock A:
- 1st: 10:00:06
- 2nd: 10:01:13
- 3rd: 9:59:00.8
- 4th: 10:02:15
- 5th: 9:58:10
- Clock B:
- 1st: 8:15:00
- 2nd: 8:15:00.1
- 3rd: 8:15:04
- 4th: 8:14:58
- 5th: 8:15:02
2. Calculate the Differences Between Readings for Clock A:
- Between 1st and 2nd: 10:01:13 - 10:00:06 = 1 minute 7 seconds
- Between 2nd and 3rd: 10:01:13 - 9:59:00.8 = 2 minutes 12.2 seconds
- Between 3rd and 4th: 10:02:15 - 9:59:00.8 = 3 minutes 14.2 seconds
- Between 4th and 5th: 10:02:15 - 9:58:10 = 4 minutes 5 seconds
3. Calculate the Differences Between Readings for Clock B:
- Between 1st and 2nd: 8:15:00.1 - 8:15:00 = 0.1 seconds
- Between 2nd and 3rd: 8:15:04 - 8:15:00.1 = 3.9 seconds
- Between 3rd and 4th: 8:14:58 - 8:15:04 = 6 seconds
- Between 4th and 5th: 8:15:02 - 8:14:58 = 4 seconds
4. Analyze the Differences:
- For Clock A, the differences between readings are significantly larger, ranging from about 1 minute to over 4 minutes.
- For Clock B, the differences are much smaller, ranging from 0.1 seconds to 6 seconds.
5. Conclusion:
- Since precision is defined as the degree of closeness of the various readings to each other, Clock B has readings that are much closer together compared to Clock A. Therefore, for experiments requiring precise time interval measurements, Clock B is the preferred choice.
- Clock A:
- 1st: 10:00:06
- 2nd: 10:01:13
- 3rd: 9:59:00.8
- 4th: 10:02:15
- 5th: 9:58:10
- Clock B:
- 1st: 8:15:00
- 2nd: 8:15:00.1
- 3rd: 8:15:04
- 4th: 8:14:58
- 5th: 8:15:02
- Between 1st and 2nd: 10:01:13 - 10:00:06 = 1 minute 7 seconds
- Between 2nd and 3rd: 10:01:13 - 9:59:00.8 = 2 minutes 12.2 seconds
- Between 3rd and 4th: 10:02:15 - 9:59:00.8 = 3 minutes 14.2 seconds
- Between 4th and 5th: 10:02:15 - 9:58:10 = 4 minutes 5 seconds
- Between 1st and 2nd: 8:15:00.1 - 8:15:00 = 0.1 seconds
- Between 2nd and 3rd: 8:15:04 - 8:15:00.1 = 3.9 seconds
- Between 3rd and 4th: 8:14:58 - 8:15:04 = 6 seconds
- Between 4th and 5th: 8:15:02 - 8:14:58 = 4 seconds
- For Clock A, the differences between readings are significantly larger, ranging from about 1 minute to over 4 minutes.
- For Clock B, the differences are much smaller, ranging from 0.1 seconds to 6 seconds.
- Since precision is defined as the degree of closeness of the various readings to each other, Clock B has readings that are much closer together compared to Clock A. Therefore, for experiments requiring precise time interval measurements, Clock B is the preferred choice.
Similar Questions
Two clocks are being tested againest a standard clock located in a national laboratory.
At 12 : 00 : 00 noon by the standard clock, the readings of the two clocks are
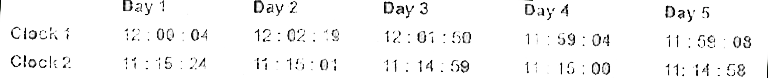
Which of the two clocks will you prefer to measure the time intervals during an experiment?
View SolutionTwo clocks are being tested against a standard clock located in a national laboratory. At 12:00:00 noon by the standard clock, the readings of the two clocks are :
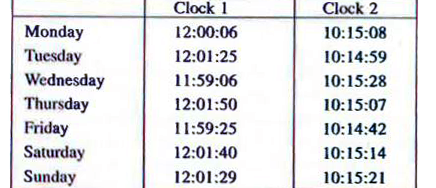
If you are doing an experiment that requires 'precision time interval' measurements , which of the two clocks will you prefer ?
View SolutionTwo clocks are being tested against a standard clock located in a national laboratory At 12 : 00 : 00 noon by standard clock, the readins of the two clocks are
DayClock - IClock - IIMonday12:00:0510:15:06Tuesday12:01:1510:14:59Wednesday11:59:0810:15:18Thursday12:01:5010:15:07Thursday12:01:5010:15:07Friday11:59:1510:14:53Saturday12:01:3010:15:24Sunday12:01:1910:15:11
From the Observations carefully read the following conclusive statements.
Statement I : Zero - error in clock II is much longer than zero - error in clock I.
Statement II : Zero - error can always be corrected by applying necessary corrective measures
Statement III : Precision of clock - I is more than precision of clock - II
Statement IV : Precision of clock - II is more than precision of clock - I
Pick up the correction option from the following.
View SolutionTwo clocks are being tsted against a standard clock located in the national laboratory. At 10:00:00 AM by the standard clock, the readings of the clocks are :

If you are doing an experiment that requires prescision time interval measurements, which of the two clock will you prefer ?
(a) Clock A
(b) Clock B
(c) Either Clock A or B
(d) Neithr A nor B
View SolutionA teacher wanted to analysis the performance of two sections of students in a mathematics test of 100 marks. Looking performance, she found that a few students got under 20 marks and a few got 70 marks or above. So she decided to group them into intervals of varying sizes as follows :
0-20, 20-30, ....., 60-70, 70-100. Then she formed the following table :
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Marks Number of students0−20 720−30 1030−40 1040−50 2050−60 2060−70 1570−above 8Total 90∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
(i) Find the probability that a student obtained less than 20% in the mathematics test.
(ii) Find the probability that a student obtained marks 60 or above .
View SolutionIn each of the following, there are three positive numbers. State if these numbers could possibly be the lengths of the sides of a triangle:
(i) 5,7,9
(ii) 2,10,15
(iii) 3,4,5
(iv) 2,5,7
(v) 5,8,20
View SolutionAn examination is taken at three centres each of which has 100 candidates. The mean marks and standard deviation for each centre are given below.
(I^(st)"centre",,45,9.6),(II^(nd)"centre",50,10.8), (III^(rd)"centre",43,9.0):}
Calculate the standard deviation of all 300 candidates.
View SolutionConsider the following values of I.E.(eV) for elements W and X:
ElementI.E1I.E2I.E3I.E4W10.515.524.979.8X814.878.9105.8
Other two element Y and Z hav outer electronic configuration ns2np4andns2np5 respectively. then according to given information which of the following compound(s) is/are not possible?
View SolutionIn the circuit shown in figure, E = 10 V, r = 1Ω,
R = 4Ω and L = 5H. The circuit is closed at time t = 0.
Then, match the following two columns.
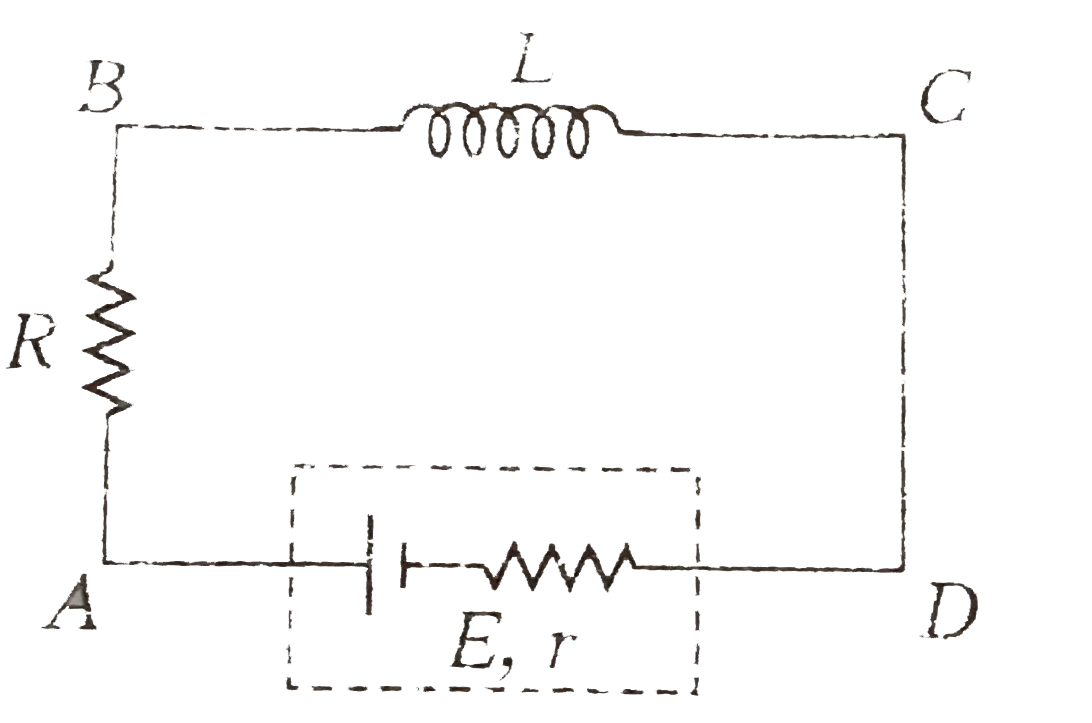
Column IColumn IIA.VAD at t = 0p4VB.VBC at t = 0q8VC.VAB at t =∞r.0VD.VAD at t=∞s.10V
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :
View Solution
