Ice pieces are floating in a beaker A containing water and also in a beaker B containing miscible liquid of specific gravity 1.2 When ice melts, the level of
Water increases in A
Water decreases in A
Liquid in B decreases
Liquid in B increases
To solve the problem regarding the melting of ice in two different liquids, we will analyze each beaker separately.
Step 1: Analyze Beaker A (Water)
- In Beaker A, ice is floating in water. The buoyant force acting on the ice is equal to the weight of the ice.
- The weight of the ice can be expressed as:
Wice=ρice⋅Vice⋅g
where ρice is the density of ice, Vice is the volume of the ice, and g is the acceleration due to gravity.
- The buoyant force is given by Archimedes' principle:
Fb=ρwater⋅Vdisplaced⋅g
where ρwater is the density of water and Vdisplaced is the volume of water displaced by the ice.
- Since the ice is floating, we have:
Wice=Fb
This implies:
ρice⋅Vice⋅g=ρwater⋅Vdisplaced⋅g
- Given that the density of ice (ρice) is less than that of water (ρwater), the volume of water displaced is equal to the volume of the ice submerged.
- When the ice melts, it turns into water. The volume of water produced from the melted ice is equal to the volume of the ice that was submerged.
Conclusion for Beaker A:
- The water level in Beaker A remains unchanged when the ice melts.
---
Step 2: Analyze Beaker B (Miscible Liquid with Specific Gravity 1.2)
- In Beaker B, ice is floating in a miscible liquid with a specific gravity of 1.2. This means the density of the liquid is:
ρliquid=1.2⋅ρwater
- Similar to Beaker A, the weight of the ice is balanced by the buoyant force:
Wice=Fb
ρice⋅Vice⋅g=ρliquid⋅Vdisplaced⋅g
- Substituting the density of the liquid:
ρice⋅Vice=1.2⋅ρwater⋅Vdisplaced
- From the above equation, we can express the volume of the displaced liquid:
Vdisplaced=ρice1.2⋅ρwater⋅Vice
- When the ice melts, the volume of water formed is equal to the volume of the ice:
Vwater=Vice
- The volume of water produced from the melted ice is greater than the volume of the liquid displaced because:
Vwater=Vice>Vdisplaced
Conclusion for Beaker B:
- The water level in Beaker B will increase when the ice melts because the volume of water produced from the melted ice is greater than the volume of the liquid that was displaced.
Final Answer:
- The level of water in Beaker A remains unchanged, while the level of liquid in Beaker B increases.
- In Beaker A, ice is floating in water. The buoyant force acting on the ice is equal to the weight of the ice.
- The weight of the ice can be expressed as:
Wice=ρice⋅Vice⋅g
where ρice is the density of ice, Vice is the volume of the ice, and g is the acceleration due to gravity.
Fb=ρwater⋅Vdisplaced⋅g
where ρwater is the density of water and Vdisplaced is the volume of water displaced by the ice.
Wice=Fb
This implies:
ρice⋅Vice⋅g=ρwater⋅Vdisplaced⋅g
- The water level in Beaker A remains unchanged when the ice melts.
- In Beaker B, ice is floating in a miscible liquid with a specific gravity of 1.2. This means the density of the liquid is:
ρliquid=1.2⋅ρwater
Wice=Fb
ρice⋅Vice⋅g=ρliquid⋅Vdisplaced⋅g
ρice⋅Vice=1.2⋅ρwater⋅Vdisplaced
Vdisplaced=ρice1.2⋅ρwater⋅Vice
Vwater=Vice
Vwater=Vice>Vdisplaced
- The water level in Beaker B will increase when the ice melts because the volume of water produced from the melted ice is greater than the volume of the liquid that was displaced.
- The level of water in Beaker A remains unchanged, while the level of liquid in Beaker B increases.
সম্পর্কিত প্রশ্ন
A piece of ice is floating in a beaker containing thick sugar solution of water. As the ice melts, the total level of he liquid
View SolutionA piece of ice is floating in a vessel containing water and inside the ice is a bubble of air. What will be the effect on the level of water, when the ice melts?
View SolutionA plece of ice floats in a beaker containing water with a certain fraction inside water. If the density of ice is D and that of water is ρ find the value of n. What will happen to the level of water when the ice completely melts ?
View SolutionAn ice cube containing a galss ball is floating on the surface of water contained in a trough. The whole of the ice melts, the level of water in the trough
View SolutionA hollow cylindrical container floats in water with half its length immersed. A liquid of specific gravity σ is slowly poured into the container until the levels of the liquid inside the container and of water outside are the same. It is observed that the container is submerged to two-thirds its length. Then the value of σ is
View SolutionA block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at 0∘C as the ice melts. When the ice melts completely the level of water in the vessel rises.
View SolutionState true/false:
S1 : Hydrostatic pressure is a scalar quantity even though pressure is force divided by area and force is a vector quantity?
S2: A barometer made of a very narrow tube (see figure) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018/.∘C and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C but the temperature of the atmosphere does not change. Then, the mercury height in the tube remains unchanged.
S3 A block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at 0∘C as the ice melts. When the ice melts completely the level of water in the vessel rises.
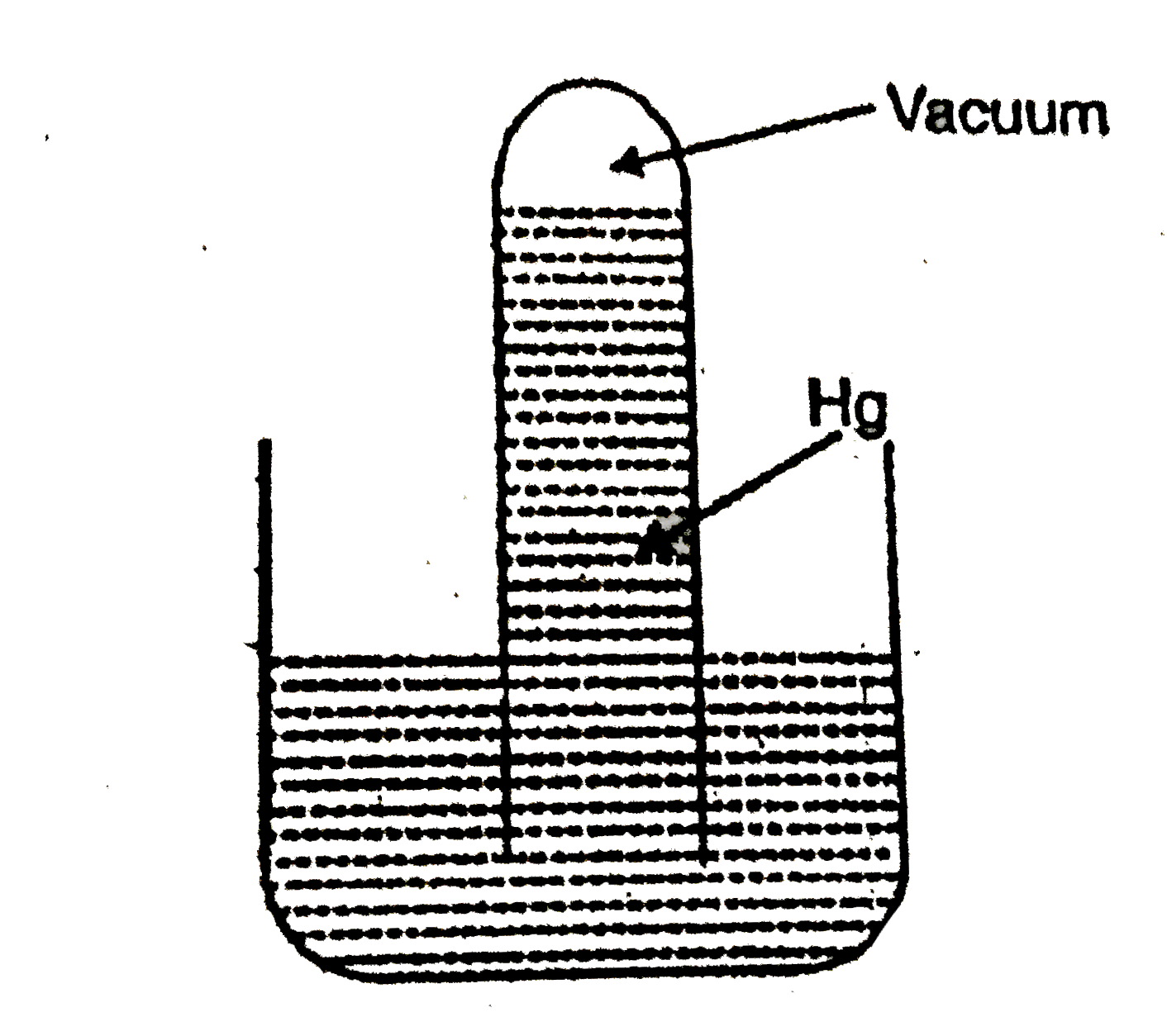
View SolutionA body floats in a liquid contained in a beaker. The whole system shown in figure is falling under gravity, the upthrust on the body due to the liquid is
View SolutionA body floats in a liquid contained in a beaker. The whole system as shown in Figure falls freely under gravity. The upthrust on the body is

View SolutionAn ice-cube of edge is 10 cm floating in water. Time period of small vertical oscillations of the cube is: (Specific gravity of ice is 0.9)
View Solution
