Two waves represented by yi=3sin(200x−150t)andy2=3cos(200x−150t) are superposed where x and y are in metre and t is in second. Calculate the amplitude of resultant wave
The correct Answer is:3√2m
To find the amplitude of the resultant wave formed by the superposition of the two waves given by y1=3sin(200x−150t) and y2=3cos(200x−150t), we can follow these steps:
Step 1: Convert the cosine wave to sine form
The wave y2 is given in cosine form. We can convert it to sine form using the identity:
cos(θ)=sin(θ+π2)
Thus, we can rewrite y2 as:
y2=3cos(200x−150t)=3sin(200x−150t+π2)
Step 2: Identify the amplitudes and phase angles
From the equations:
- For y1=3sin(200x−150t):
- Amplitude a1=3
- Phase angle ϕ1=0
- For y2=3sin(200x−150t+π2):
- Amplitude a2=3
- Phase angle ϕ2=π2
Step 3: Calculate the phase difference
The phase difference Δϕ between the two waves is:
Δϕ=ϕ2−ϕ1=π2−0=π2
Step 4: Use the formula for resultant amplitude
The resultant amplitude A of two superposed waves can be calculated using the formula:
A=√a21+a22+2a1a2cos(Δϕ)
Substituting the values:
A=√32+32+2⋅3⋅3⋅cos(π2)
Step 5: Calculate the cosine term
Since cos(π2)=0, the equation simplifies to:
A=√32+32+0=√9+9=√18
Step 6: Simplify the resultant amplitude
A=√18=3√2
Final Result
Thus, the amplitude of the resultant wave is:
3√2
The wave y2 is given in cosine form. We can convert it to sine form using the identity:
cos(θ)=sin(θ+π2)
Thus, we can rewrite y2 as:
y2=3cos(200x−150t)=3sin(200x−150t+π2)
From the equations:
- For y1=3sin(200x−150t):
- Amplitude a1=3
- Phase angle ϕ1=0
- Amplitude a2=3
- Phase angle ϕ2=π2
The phase difference Δϕ between the two waves is:
Δϕ=ϕ2−ϕ1=π2−0=π2
The resultant amplitude A of two superposed waves can be calculated using the formula:
A=√a21+a22+2a1a2cos(Δϕ)
Substituting the values:
A=√32+32+2⋅3⋅3⋅cos(π2)
Since cos(π2)=0, the equation simplifies to:
A=√32+32+0=√9+9=√18
A=√18=3√2
Thus, the amplitude of the resultant wave is:
3√2
Topper's Solved these Questions
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-A)
55 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-B)
35 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Video
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
Similar Questions
The types of mechanical wave we expect the exist in vacuum is
View SolutionIf consecutive freuquencies emitted from an organ pipe are 50 Hz, 75Hz, 100 Hz, 125 Hz, then the frequency of the 10th overtone is
View SolutionA : Doppler's effect in sound is asymmetric but in light , it is symmetric
R : In Sound , change in frequency depends on the individual velocity of both the source as well as the observer . In light , change in frequency depends on the relative velocity between source and observer .
View SolutionA point source S emitting light of wavelength 600 nm is placed at a very small height h above a flat figure. The intensity of the reflected light id 36% of the incident intensity. Interference fringe are observed on a screen placed parallel to the reflecting surface at a very large distance D from it.
a. What is the shape of the interference fringe on the screen?
b. Calculate the ratio of the minimum to the maximum intensities in the interference fringes formed near point P (shown in the figure).
c. If the intensity at point P corresponds to a maximum, calculate the mininum distance through which the reflecting surface. AB should at P again becomes maxinum.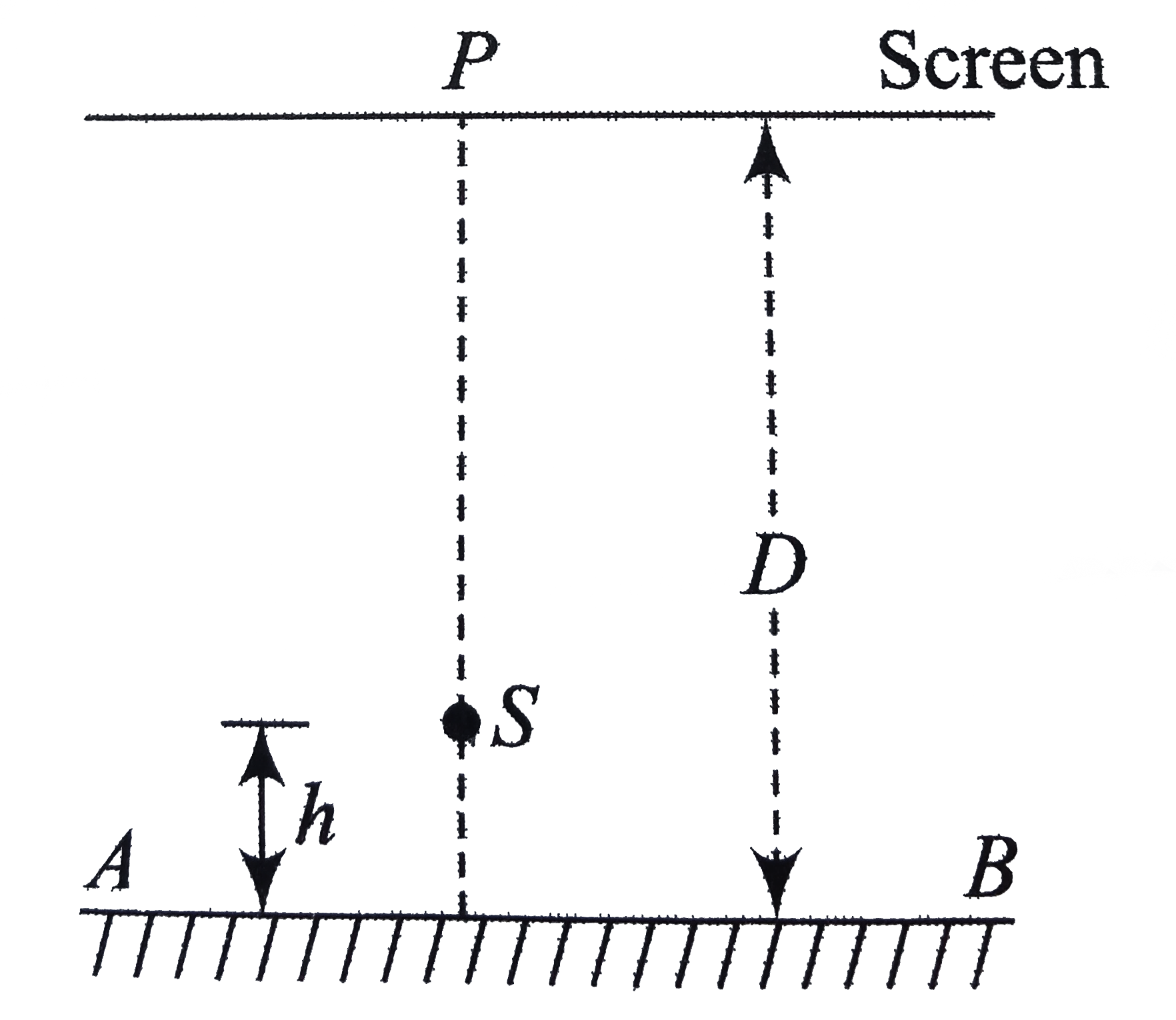
View SolutionA : The work done by a force during round trip is always zero.
R : The average value of force in round trip is zero.
View SolutionA wave is represented by the equetion
y=y0sin[10πx−15πt+(π/3)]
where x is in metres and t in seconds. The equation represent a travelling wave:
View SolutionIf two waves represented by y1=4sinωt and y2=3sin(ωt+π3) interfere at a point find out the amplitude of the resulting wave
View SolutionTwo waves are represented by y_(1)= a sin (omega t + ( pi)/(6)) and y_(2) = a cos omega t . What will be their resultant amplitude
View SolutionIf two waves represented by y_(1)=4 sin omega t and y_(2)=3sin (omega t+(pi)/(3)) interfere at a point, the amplitude of the resulting wave will be about
View SolutionTwo waves represented by yi=3sin(200x−150t)andy2=3cos(200x−150t) are superposed where x and y are in metre and t is in second. Calculate the amplitude of resultant wave
View SolutionEquations of two light waves are y1= 4 sin ω t and y2=3sin(ωt+π2). What is the amplitude of the resultant wave as they superpose on each other?
View Solutiony_(1)=Asin(omegat-kx)&y_(2)=Asin(omegat-kx+delta) : these two equations are representing two waves. Then the amplitude of the resulting wave is
View SolutionTwo waves represented by yi=3sin(200x−150t)andy2=3cos(200x−150t) are superposed where x and y are in metre and t is in second. Calculate the amplitude of resultant wave
View SolutionTwo waves represented as y_(1) = A_(1) sin omega t and y_(2) = A_(2) cos omega t superpose at a point in space. Find out the amplitude of the resultant wave at that point .
View SolutionWhen the waves y_(1) = A sin omega t and y_(2) = A cos omega t are superposed, then resultant amplitude will be
View Solution

