The force of a particle of mass 1 kg is depends on displacement as F = —4x then the frequency of S.H.M. is
πHz
2πHz
1πHz
12πHz
The correct Answer is:C
To solve the problem, we need to find the frequency of the simple harmonic motion (SHM) for a particle of mass 1 kg, given that the force acting on it is F=−4x.
1. Identify the Force Equation:
The force acting on the particle is given by:
F=−4x
This is in the form of Hooke's law, which states that F=−kx, where k is the spring constant.
2. Determine the Spring Constant k:
By comparing the given force equation with the standard form F=−kx, we can identify that:
k=4N/m
3. Use the Formula for Time Period T:
The time period T of SHM is given by the formula:
T=2π√mk
where m is the mass of the particle and k is the spring constant.
4. Substitute the Values:
Here, the mass m=1kg and k=4N/m. Substituting these values into the formula gives:
T=2π√14=2π⋅12=πs
5. Calculate the Frequency f:
The frequency f is the reciprocal of the time period T:
f=1T=1πHz
Final Answer:
The frequency of the simple harmonic motion is:
f=1πHz
The force acting on the particle is given by:
F=−4x
This is in the form of Hooke's law, which states that F=−kx, where k is the spring constant.
By comparing the given force equation with the standard form F=−kx, we can identify that:
k=4N/m
The time period T of SHM is given by the formula:
T=2π√mk
where m is the mass of the particle and k is the spring constant.
Here, the mass m=1kg and k=4N/m. Substituting these values into the formula gives:
T=2π√14=2π⋅12=πs
The frequency f is the reciprocal of the time period T:
f=1T=1πHz
The frequency of the simple harmonic motion is:
f=1πHz
Topper's Solved these Questions
Similar Questions
Power of the only force acting on a particle of mass m=1 kg moving in straight line depends on its velocity as P=v2 where v is in m/s and P is in watt. If initial velocity of the particle is 1m/s, then the displacement of the particle in ln2 second will be :
View SolutionThe equation of S.H.M. of a particle is a+4π2x=0, where a is instantaneous linear acceleration at displacement x. Then the frequency of motion is
View SolutionA particle of mass 1 kg is moving in SHM with path length 0.01 m and a frequency of 50 Hz. The maximum force in newton, acting on the particle is
View SolutionThe figure shows the position time graph of a particle of mass 40 kg. What is the force acting on the particle of 0<t<4 s
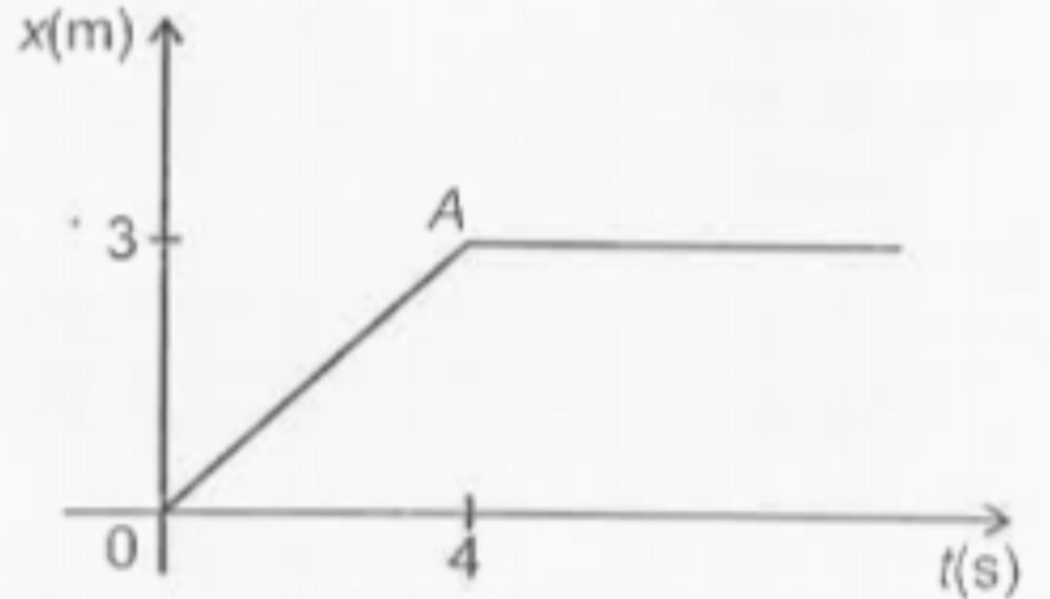
View SolutionA force F acting on a body depends on its displacement S as F∝S−1/3 . The power delivered by F will depend on displacement as
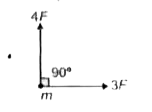
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
View SolutionThe potential energy of a particle of mass 2 kg in SHM is (9x2)J. Here x is the displacement from mean position . If total mechanical energy of the particle is 36 J. The maximum speed of the particle is
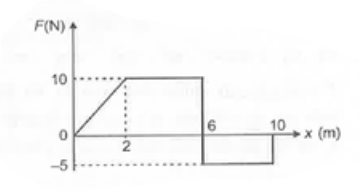
View SolutionThe force versus position (F-x) graph of a particle of mass 2 kg is shown in the figure. If at x = 0 velocity of particle is 2 m/s then velocity of the particle at x = 8 m will be
View SolutionThe displacement 'x' (in meter) of a particle of mass 'm' (in kg) moving in one dimension under the action of a force is released to time 't' (in sec) by t2=√x+2. The displacement of the particle when its velocity is zero will be.
View SolutionA time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
View Solution

