A particle of mass 300 g is moving with a speed of 20 ms−1 along the straight line y = x - 4√2. The angular momentum of the particle about the origin is (where y & x are in metres)
The correct Answer is:A
To find the angular momentum of a particle about the origin, we can follow these steps:
Step 1: Identify the mass and speed of the particle
The mass m of the particle is given as 300 g, which we need to convert to kilograms:
m=300g=0.3kg
The speed v of the particle is given as:
v=20m/s
Step 2: Determine the equation of the line and find points of intersection with axes
The particle is moving along the line given by the equation:
y=x−4√2
To find the points where this line intersects the axes, we can set x=0 to find the y-intercept:
y=0−4√2=−4√2
So, the point of intersection with the y-axis is (0,−4√2).
Next, we set y=0 to find the x-intercept:
0=x−4√2⟹x=4√2
So, the point of intersection with the x-axis is (4√2,0).
Step 3: Find the slope of the line
The slope m of the line can be calculated using the two points found:
- Point A: (0,−4√2)
- Point B: (4√2,0)
The slope m is given by:
m=y2−y1x2−x1=0−(−4√2)4√2−0=4√24√2=1
Step 4: Find the coordinates of the particle's position
The equation of the line can be rewritten in slope-intercept form:
y=x−4√2
To find the coordinates of the particle at a specific time, we can use the fact that it moves with a speed of 20 m/s along this line.
Step 5: Calculate the position vector →R
Assuming the particle is at point (x,y) at time t, we can express R as:
R=√x2+y2
Using the coordinates (2√2,−2√2) (found in the video transcript), we calculate:
R=√(2√2)2+(−2√2)2=√8+8=√16=4m
Step 6: Calculate the angular momentum L
The angular momentum L about the origin is given by the formula:
L=m⋅v⋅R
Substituting the known values:
L=0.3kg⋅20m/s⋅4m
Calculating this gives:
L=0.3⋅20⋅4=24kg m2/s
Final Answer
The angular momentum of the particle about the origin is:
24kg m2/s
The mass m of the particle is given as 300 g, which we need to convert to kilograms:
m=300g=0.3kg
The speed v of the particle is given as:
v=20m/s
The particle is moving along the line given by the equation:
y=x−4√2
To find the points where this line intersects the axes, we can set x=0 to find the y-intercept:
y=0−4√2=−4√2
So, the point of intersection with the y-axis is (0,−4√2).
0=x−4√2⟹x=4√2
So, the point of intersection with the x-axis is (4√2,0).
The slope m of the line can be calculated using the two points found:
- Point A: (0,−4√2)
- Point B: (4√2,0)
m=y2−y1x2−x1=0−(−4√2)4√2−0=4√24√2=1
The equation of the line can be rewritten in slope-intercept form:
y=x−4√2
To find the coordinates of the particle at a specific time, we can use the fact that it moves with a speed of 20 m/s along this line.
Assuming the particle is at point (x,y) at time t, we can express R as:
R=√x2+y2
Using the coordinates (2√2,−2√2) (found in the video transcript), we calculate:
R=√(2√2)2+(−2√2)2=√8+8=√16=4m
The angular momentum L about the origin is given by the formula:
L=m⋅v⋅R
Substituting the known values:
L=0.3kg⋅20m/s⋅4m
Calculating this gives:
L=0.3⋅20⋅4=24kg m2/s
The angular momentum of the particle about the origin is:
24kg m2/s
Topper's Solved these Questions
Similar Questions
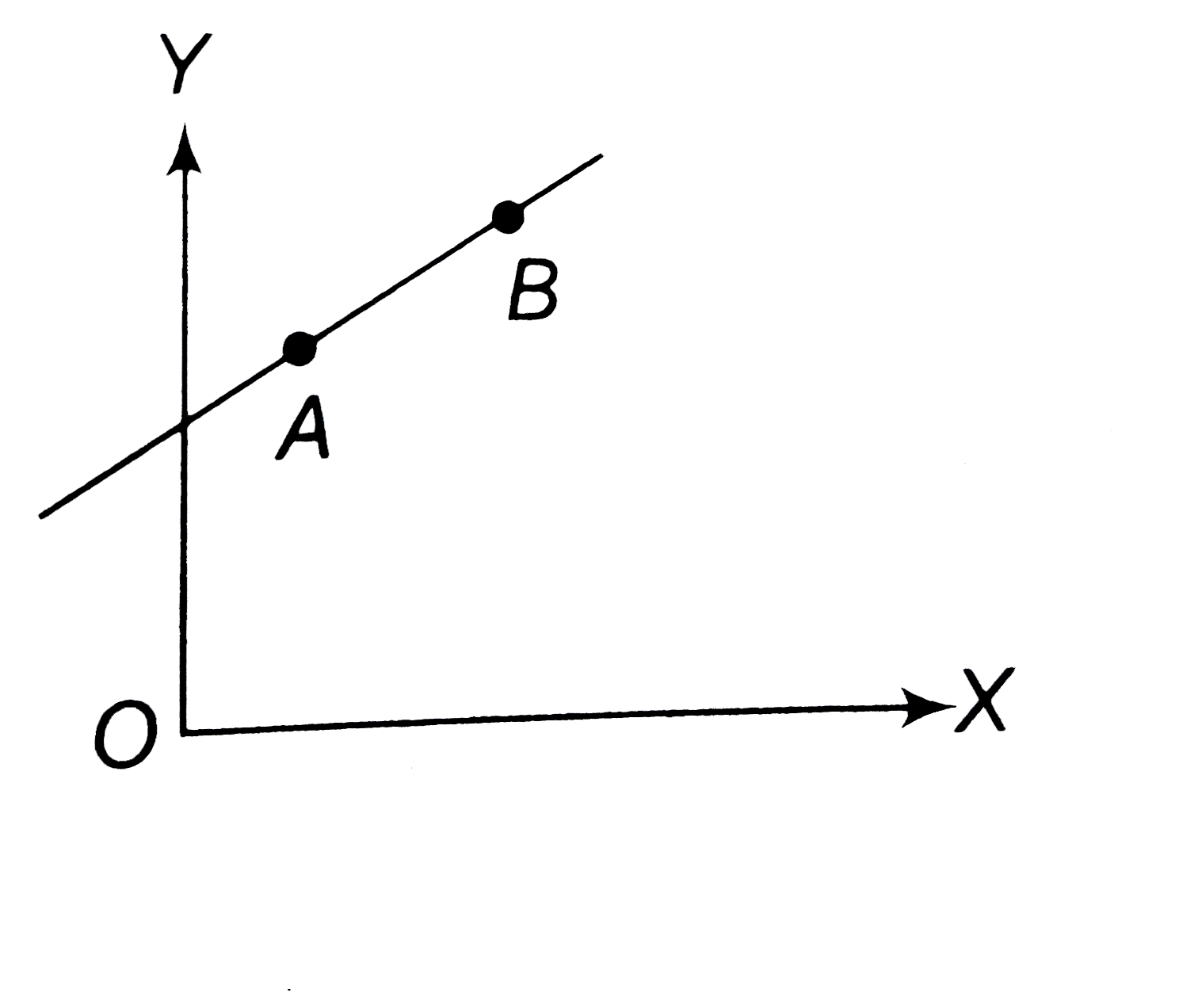
A particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then
View SolutionA particle of mass 5g is moving with a uniform speed of 3√2cm/s in the x−y plane along the line y=x+4. The magnitude of its angular momentum about the origin in gcm2/s is
View SolutionA particle of mass 5 g is moving with a uniform speed of 3√2cm s−1 in the XY-plane along the line y=2√5 cm. The magnitude of its angular momentum about the origin in g-cm2s−1 is
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass 1 kg is moving along the line y=x+2 (here x and y are in metres) with speed 2m/s. The magnitude of angular momentum of paticle about origin is -
View SolutionA particle of mass m=5 units is moving with a uniform speed v=3√2 units in the XY-plane along the y=x+4. The magnitude of the angular momentum about origin is
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
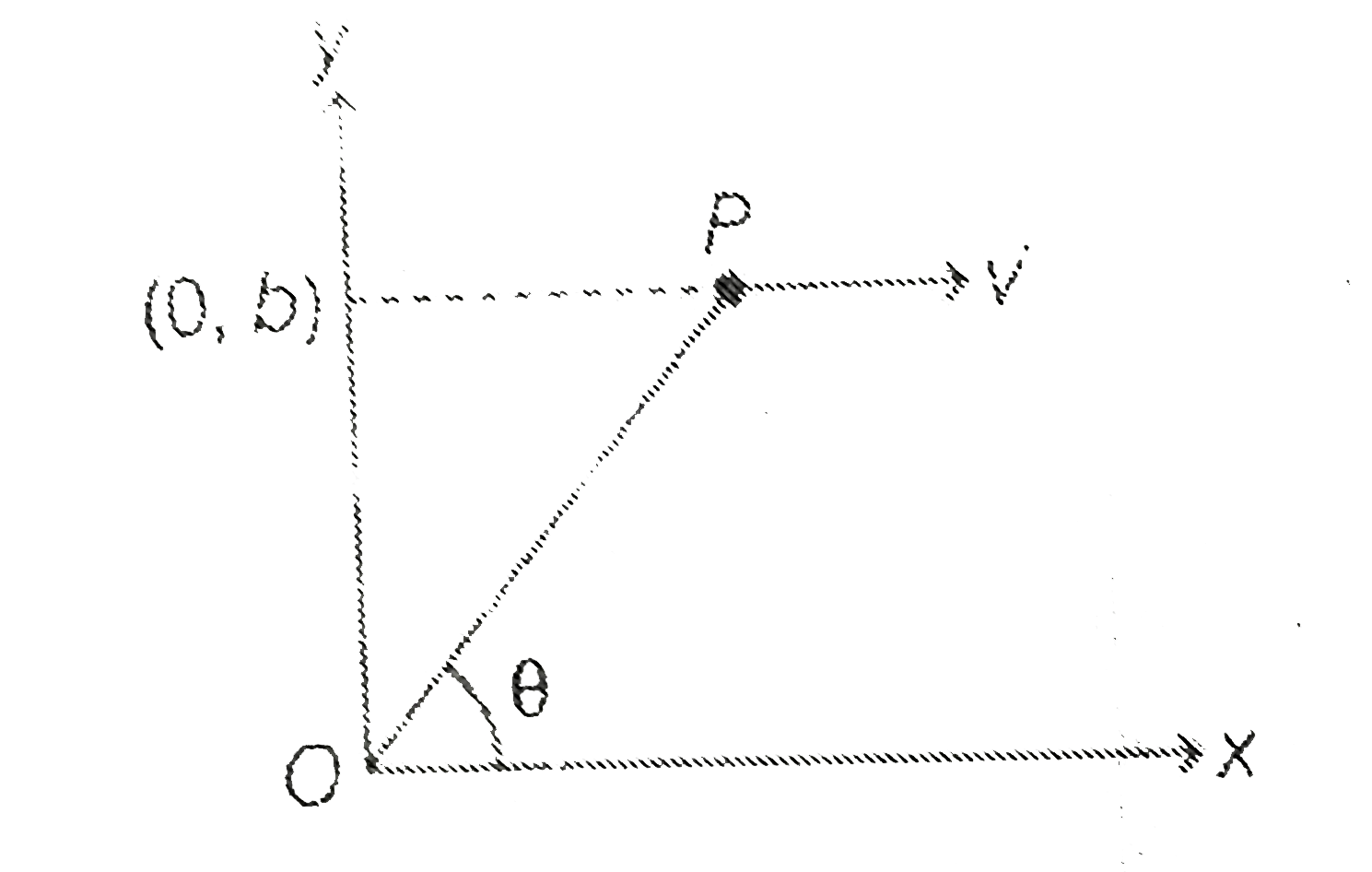
View SolutionA particle of mass m is moving along the line y=b,z=0 with constant speed v. State whether the angular momentum of particle about origin is increasing, decreasing or constant.
View SolutionA particle of mass m is moving along the line y=b,z=0 with constant speed v. State whether the angular momentum of particle about origin is increasing. Decreasing or constant.
View Solution

