In a circle of radius 5 cm, PQ and RS are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are on:
opposite sides of the centre.
The correct Answer is:7cm
To solve the problem, we need to find the distance between two parallel chords, PQ and RS, in a circle of radius 5 cm, where the lengths of the chords are 8 cm and 6 cm respectively, and they are on opposite sides of the center.
1. Identify the Circle and Chords:
- We have a circle with a radius of 5 cm.
- Chord PQ has a length of 8 cm.
- Chord RS has a length of 6 cm.
- Both chords are parallel and on opposite sides of the center of the circle.
2. Find the Midpoints of the Chords:
- Let A be the midpoint of chord PQ and B be the midpoint of chord RS.
- Since PQ is 8 cm long, the length from the center to A (denoted as AQ) is half of 8 cm:
AQ=82=4 cm
- Similarly, for chord RS which is 6 cm long, the length from the center to B (denoted as BS) is half of 6 cm:
BS=62=3 cm
3. Apply the Pythagorean Theorem:
- In triangle OAQ (where O is the center of the circle), we can apply the Pythagorean theorem:
OQ2=OA2+AQ2
where OQ is the radius (5 cm):
52=OA2+42
25=OA2+16
OA2=25−16=9
OA=√9=3 cm
- Now, for triangle OBS (where B is the midpoint of chord RS):
OS2=OB2+BS2
where OS is also the radius (5 cm):
52=OB2+32
25=OB2+9
OB2=25−9=16
OB=√16=4 cm
4. Calculate the Distance Between the Chords:
- Since the chords are on opposite sides of the center, the total distance between the chords PQ and RS is:
AB=OA+OB=3 cm+4 cm=7 cm
Final Answer:
The distance between the chords PQ and RS is 7 cm.
- We have a circle with a radius of 5 cm.
- Chord PQ has a length of 8 cm.
- Chord RS has a length of 6 cm.
- Both chords are parallel and on opposite sides of the center of the circle.
- Let A be the midpoint of chord PQ and B be the midpoint of chord RS.
- Since PQ is 8 cm long, the length from the center to A (denoted as AQ) is half of 8 cm:
AQ=82=4 cm
- Similarly, for chord RS which is 6 cm long, the length from the center to B (denoted as BS) is half of 6 cm:
BS=62=3 cm
- In triangle OAQ (where O is the center of the circle), we can apply the Pythagorean theorem:
OQ2=OA2+AQ2
where OQ is the radius (5 cm):
52=OA2+42
25=OA2+16
OA2=25−16=9
OA=√9=3 cm
OS2=OB2+BS2
where OS is also the radius (5 cm):
52=OB2+32
25=OB2+9
OB2=25−9=16
OB=√16=4 cm
- Since the chords are on opposite sides of the center, the total distance between the chords PQ and RS is:
AB=OA+OB=3 cm+4 cm=7 cm
The distance between the chords PQ and RS is 7 cm.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:STATISTICS
Explore 5 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:MEAN AND MEDIAN
Explore 4 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:AREA
Explore 5 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Graphical solution
Explore 10 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(D)
Explore 12 Videos
Similar Questions
Construct a cumulative frequency distribution table from the following frequency table :
C.IFrequency 11−201521−302131−402641−501851−601361−7015
View SolutionFind the mean of the following numbers.
16 14 12 8 23 26
18 20 23 9 11 22
27 18 and 20
State the value of the mean when each of these numbers is :
(i) increased by 4.
(ii) decreased by 6.
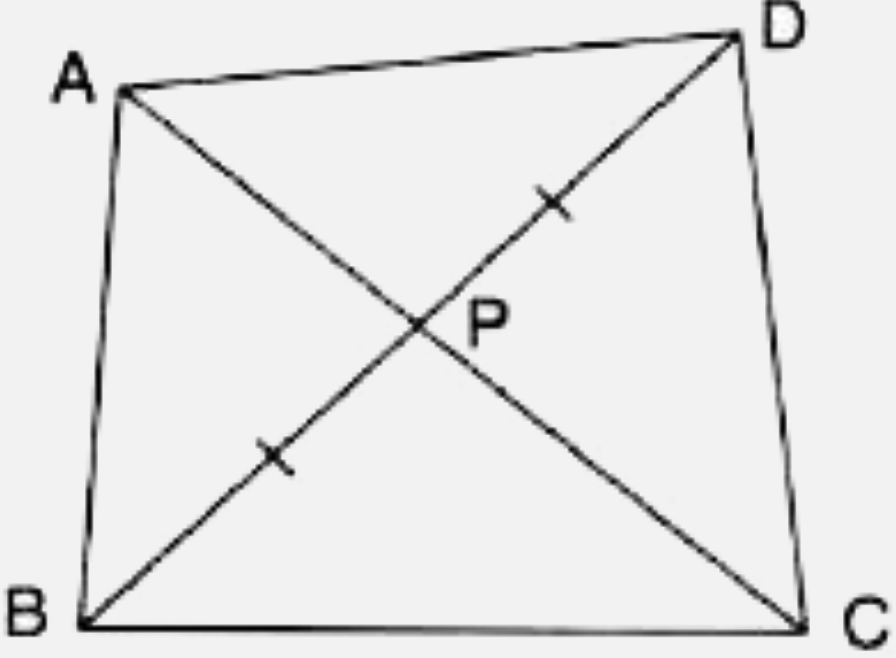
View SolutionIn quadrilateral ABCD, diagonal BD is bisected by the diagonal AC. Prove that : ΔABCandΔADC are equal in area.
View SolutionSolve the following paris of linear (simultaneous) equation using method of elimination by substution:
2x - 3y = 7
5x + y = 9
View SolutionThe radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centres.
View SolutionThe length of two parallel chords of a circle are 6 cm and 8 cm . The radius of the circle is 5 cm. Find the distance btween them if :
(i) chords are on the same side of the centre.
(ii) chords are on the opposite side of the centre.
View SolutionIn a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are
(i) on the same side of the centre.
(ii) on the opposite sides of the centre.
View SolutionTwo chords AB and CD of length 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo parallel chords of a circle, of diameter 20 cm lying on the opposite sides of the centre are of lengths 12 cm and 16 cm . The distance between the chords is
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.

View SolutionPQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ = 16 cm and RS = 12 cm, find the distance between PQ and RS, if they lie on the same side of the centre O.
View Solution