Two circles touch each other internally at point P. QPR is the tangent at P, segments PAB and PCD meet circles at points, A,B,C and D as shown in the figure.
Show that chord AC is parallel to chord BD.
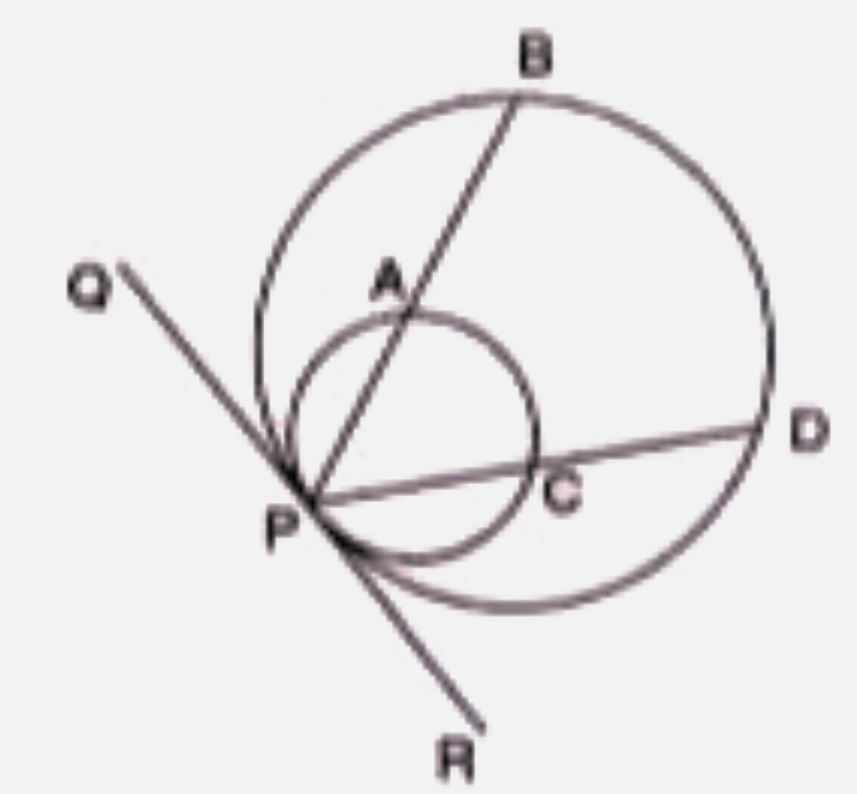
The correct Answer is:AC is parallel to BD.
Step by step video solution for Two circles touch each other internally at point P. QPR is the tangent at P, segments PAB and PCD meet circles at points, A,B,C and D as shown in the figure. Show that chord AC is parallel to chord BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18(A)
Explore 24 Videos
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (B)
Explore 18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)Book:ICSEChapter:SPECIMEN QUESTION PAPER (MATHEMATICS)Exercise:Section C
Explore 12 Videos
- TRIGONOMETRICAL IDENTITIESBook:ICSEChapter:TRIGONOMETRICAL IDENTITIESExercise:QUESTIONS
Explore 22 Videos
Similar Questions
Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
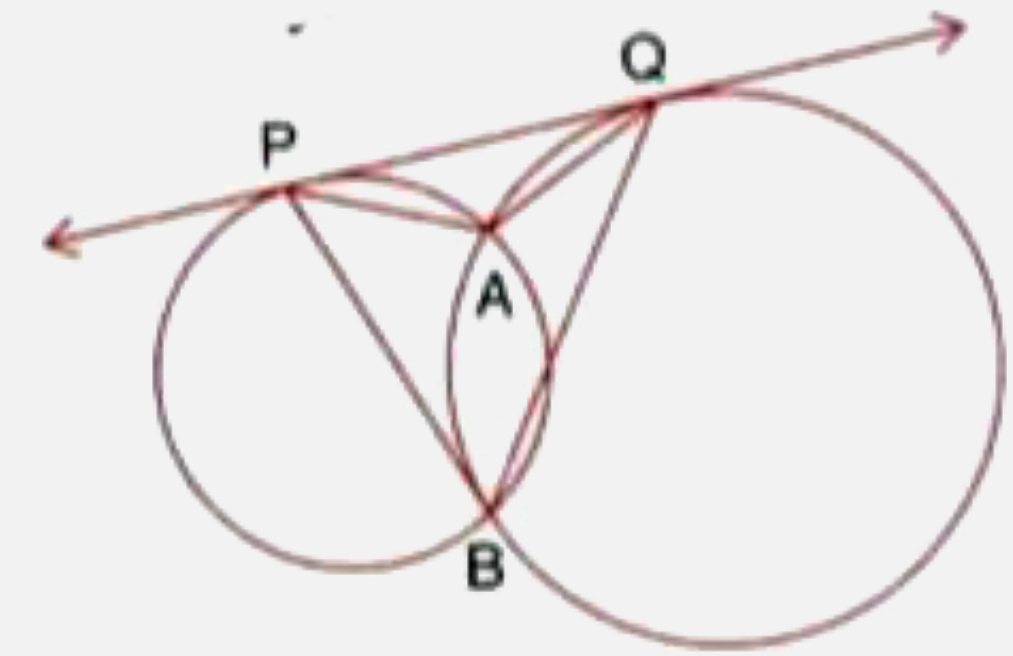
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
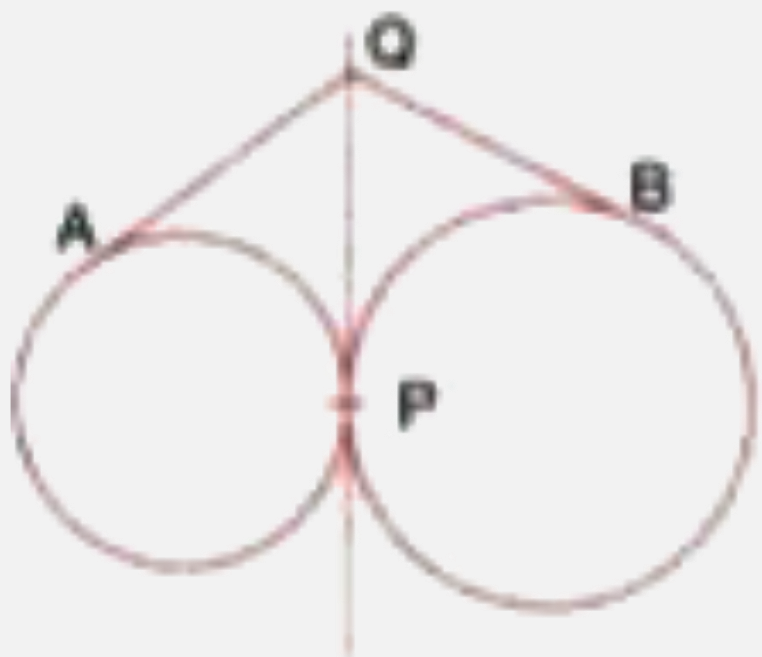
View Solution
Knowledge Check
In the figure, a,b,c,d,e,f,g,h,i, and j are chords of the circle. Which two chords are parallel to each other?
 Aa and fBb and gCc and hDe and f
Aa and fBb and gCc and hDe and f
Two circles touch each other extermally at point P. APC and BPD are straight lines. Show that :
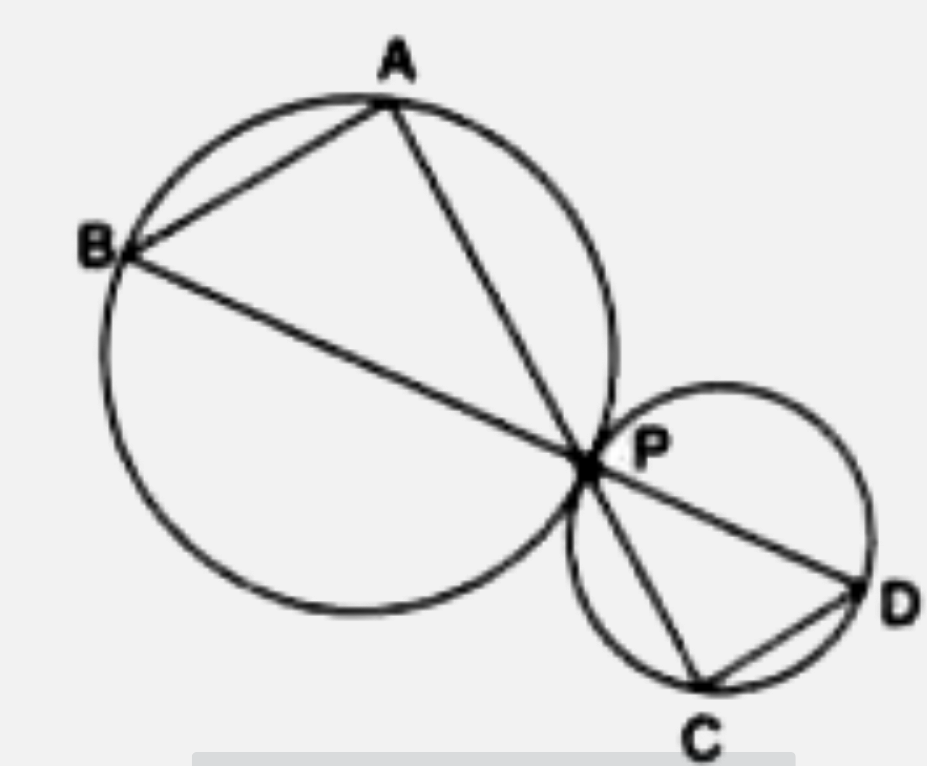
ΔPABandΔPCD are similar
View SolutionTwo circles touch each other extermally at point P. APC and BPD are straight lines. Show that :

AP is parallel to CD.
View SolutionTwo circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.
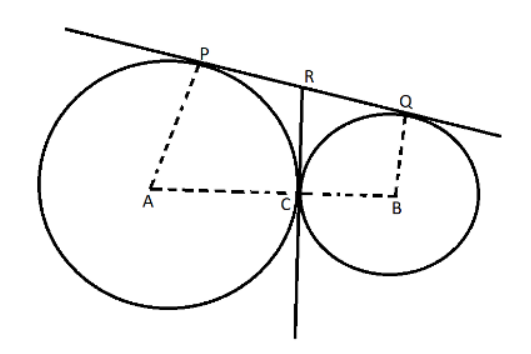
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
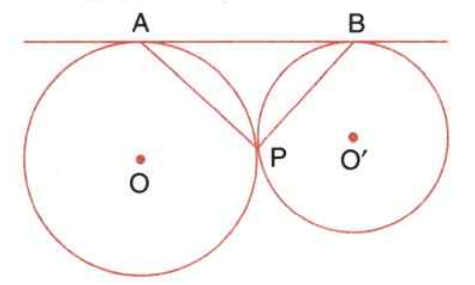
(i) tangent at point P bisects AB
(ii) angle APB=90∘
View SolutionTwo circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
View Solution