Two particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
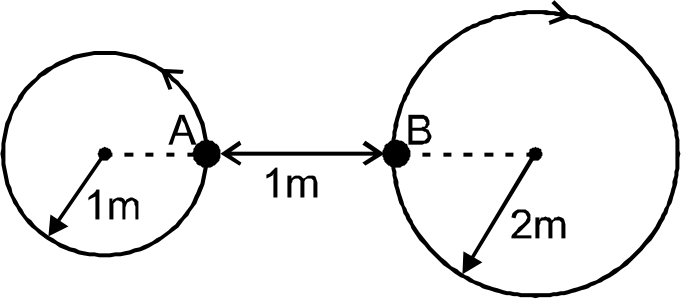
At time t=2 second, the angular velocity of the particle A with respect to the particle B is
π23m/s
π27
π24
None of these
At time t=1 s positions of A and B are
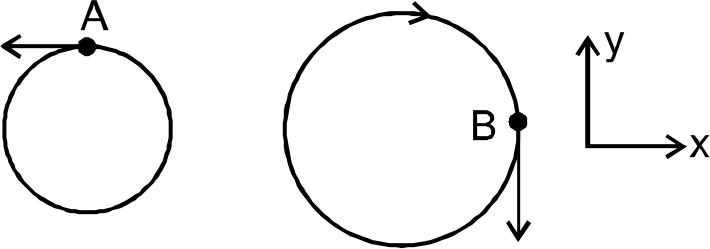
Acceleration of A →aA=ω21r1(−ˆj)=(π2)2(1)(−ˆj)
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionParticles A and B move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B , if the angular velocity of particle A w.r.t. O is omega . .
View SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are theta_(A)=((pi)/2t) and theta_(B)=(pit) respectively. here theta is in radian and t is in second. Radius of each circle is shown in diagram. Find the magnitude of acceleration of A at t=1 sec
View SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are theta_(A)=((pi)/2t) and theta_(B)=(pit) respectively. here theta is in radian and t is in second. Radius of each circle is shown in diagram. At time t=1 sec. the magnitude of acceleration of A with respect to B is
View SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.

At time t=2 second, the angular velocity of the particle A with respect to the particle B is
View SolutionA particle 'A' moves along a circle with a velocity v=at , where a=0.50m//s^(2) . Another particle B moves along a diameter OO' of the circle with the velocity v=at . Both the particles start simultaneously at t=0 from the point O on the circle. For these particles, (the radius of circle =1m ).
View SolutionFor a particle moving in a horizontal circle with constant angular velocity:
View SolutionThree particles A, B and C move in a circle of radius r=1πm, in anti-clockwise direaction with speed 1ms−1,2.5ms−1 and 2ms−1 respectively. The initial position of A, B and C are as shown in figure.
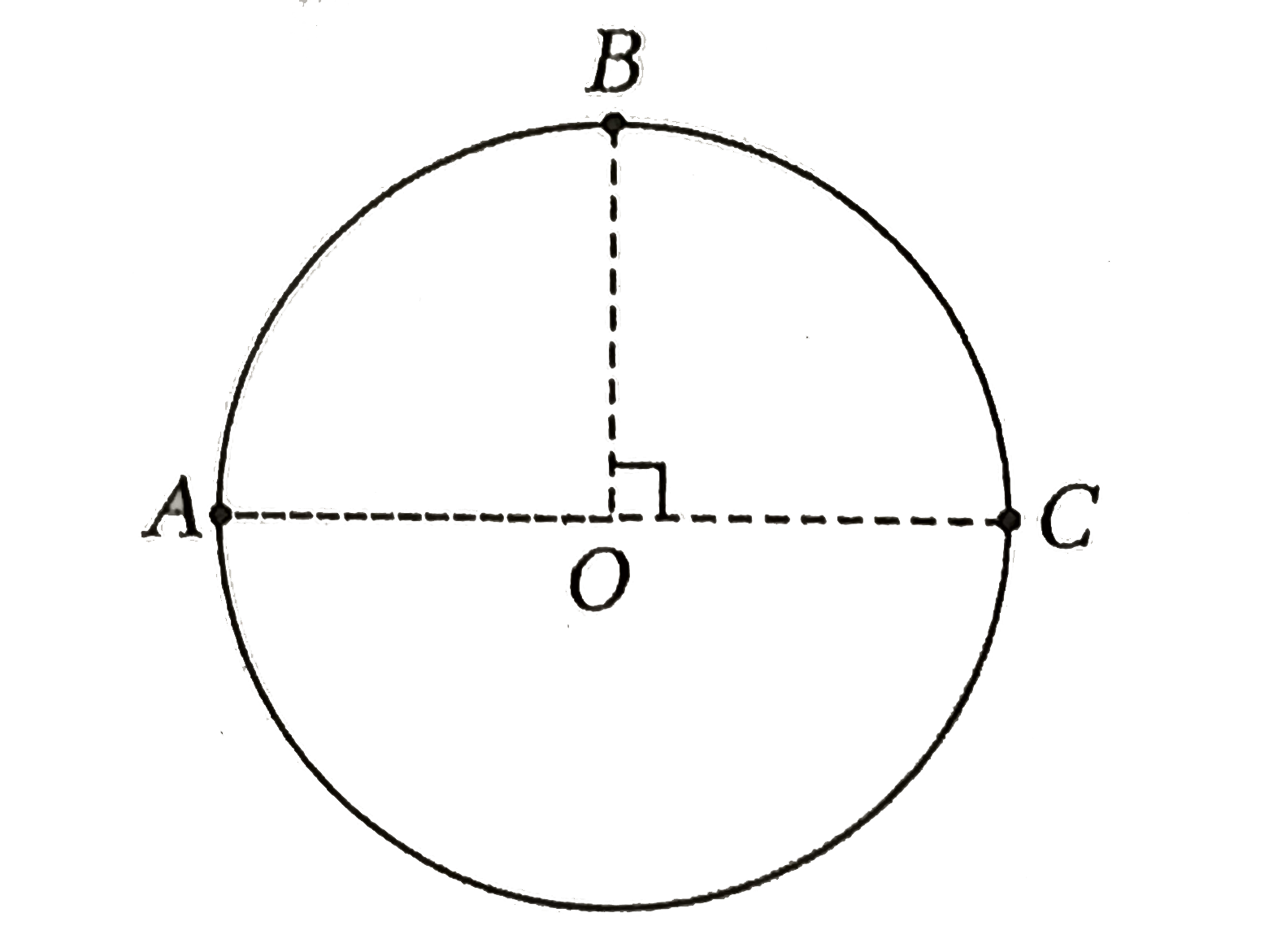
The ratio of distance travelled by B and C by the instant A, B and C meet for the first time is
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
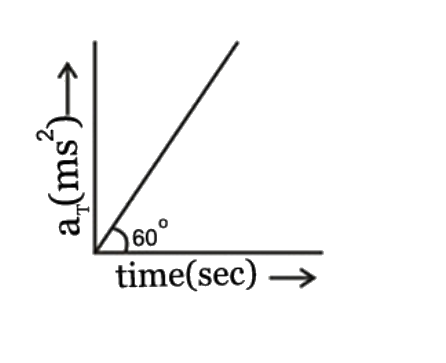
View SolutionTangential acceleration of a particle moving on a circle of radius 1 m varies with time t as shown in the graph (initial velocity of particle is zer). Time after which total acceleration of particle makes an angle of 30^@ with radial acceleration is,
View SolutionA particle is moving in a circle in front of a plane mirror in the situation as shown in figure. The plane of motion of the particle is perpendicular to the plane of mirror. Then the motion of image of particle with respected to the particle is

View SolutionThree particles A, B and C move in a circle of radius r=(1)/(pi) m, in anti-clockwise direaction with speed 1ms^(-1), 2.5ms^(-1) and 2ms^(-1) respectively. The initial position of A, B and C are as shown in figure. The ratio of distance travelled by B and C by the instant A, B and C meet for the first time is
View SolutionTwo particles are moving in different angles (in the same plane) in different angular velocities as pictured. The initial position of particles A and B at t = 0 is given by the point in the corresponding cases. The initial distance between the particles is 1m. Particle A rotates counterclockwise in the first vata and B rotates clockwise in the second vata. Time by A and B. Denoted in (rotated) angles respectively theta_(A)=((pi)/(2)t) And theta_(B)=(pit) is. here theta Is in radians and t is in the second unit. The radius of each vata is as shown in the figure- At time t = 1 sec, the magnitude of A's acceleration relative to B will be:
View SolutionTwo particles are moving in different angles (in the same plane) in different angular velocities as pictured. The initial position of particles A and B at t = 0 is given by the point in the corresponding cases. The initial distance between the particles is 1m. Particle A rotates counterclockwise in the first vata and B rotates clockwise in the second vata. Time by A and B. Denoted in (rotated) angles respectively theta_(A)=((pi)/(2)t) And theta_(B)=(pit) is. here theta Is in radians and t is in the second unit. The radius of each vata is as shown in the figure- At time t = 32 seconds the angular velocity of A will be relative to B:
View SolutionParticles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
View Solution
