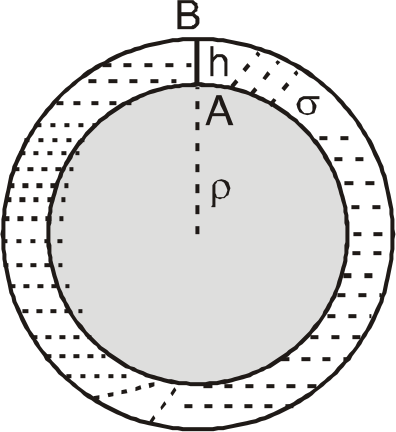
Suppose the earth was covered by an oceam of uniform depth h,(h<<R) Let σ be densityof ocean and p be mean density of earth. Let Δg be the approxemate difference of value of net acceleration duet to gravity between the bottom of the ocean and top (Δg=gtop−gbottom). Choose the correct option.
Δg=43πGh[2p−3σ]
Δg=43Gπh[3σ−2p]
Δg=43Gπh[2σ−3σ]
Δg=43Gπh[3p−3σ]
gA=43GπRp
ge=G[43πpR3+[43π(R+h)3−43πR2]σ](R+h)2
=43GπpR[1−2hR]43Gπ[(R+h)−(1−2hR)R]σ
Δg=gB−9A=43πGh[3σ−2p]
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionIf ge is acceleration due to gravity on earth and gm is acceleration due to gravity on moon, then
View SolutionSuppose the earth was covered by an oceam of uniform depth h,(h<<R) Let σ be densityof ocean and p be mean density of earth. Let Δg be the approxemate difference of value of net acceleration duet to gravity between the bottom of the ocean and top (Δg=g+(top)−gbottom). Choose the correct option.
View SolutionThe value of acceleration due to gravity 'g' on the surface of a planet with radius double that of the earth and same mean density as that of the earth is ( g_(e) =acceleration due to gravity on the surface of the earth )
View SolutionIf earth is supposed to be sphere of radius R, if g30 is value of acceleration due to gravity at latitude of 30∘ and g at the equator, then value of g−g30∘ is
View SolutionIf earth is supposed to be sphere of radius R, if g_(20) is value of acceleration due to gravity at latitude of 30^(@) and g at the equator, then value of g-g_(30^(@)) is
View SolutionLet A and B be the points respectively above and below the earth's surface each at a distance equal to half the radius of the earth. If the acceleration due to gravity at these points be gAandgB respectivel, them gB:gA
View SolutionIf g_(1) and g_(2) denote acceleration due to gravity on the surface of the earth and on a planet whose mass and radius is thrice that of earth, then
View SolutionProve that gh=g(1−2hR), where gh is the acceleration due to gravity at altitude h and h<<R (R is the radikus of the Earth).
View SolutionLet g_(h) and g_(d) the acceleration due to gravity at height h above the earth s surface and at depth d below the earth surface respecitively if g_(n) = g_(d) then the releation between h and d is
View SolutionLet gh and gd be the acceleartion due to gravity at height h above the earth s surface and at depth d below the earth 's surface respectively if gh=gd then the relation between h and d is
View SolutionSuppose the earth was covered by an ocean of uniform depth h,(h<<R) Let σ be density of ocean and p be mean density of earth. Let Δg be the approximate difference of value of net acceleration duet to gravity between the bottom of the ocean and top (Δg=g+(top)−gbottom). Choose the correct option.
View SolutionThe acceleration due to gravity at the surface of earth (g_(e)) and acceleration due to gravity at the surface of a planet (g_(p)) are equal. The density of the planet is three times than that of earth. The ratio of radius of earth to the radius of planet will be.
View SolutionThe value of acceleration due to gravity .gp. on the surface of a planet with radius double that of earth and same mean density as that of the earth is ( ge→ acceleration due to gravity on the surface of earth)
View SolutionChoose the right option: - Gravity acceleration increases / decreases with increasing depth (assuming the earth is a sphere of uniform density).
View Solution

