The acceleration of a particle moving in straight line is defined by the relation a=−4x(−1+14x2), where a is acceleration in m/s2 and x is position in meter. If velocity v=17m/s when x=0, then the velocity of the particle when x=4 meter is :
12m/s
15m/s
20m/s
25m/s
The correct Answer is:B
To solve the problem, we need to find the velocity of a particle when its position x=4 meters, given the acceleration function and the initial conditions.
1. Understand the given acceleration equation:
The acceleration a is given by:
a=−4x(−1+14x2)
This can be rewritten as:
a=−4x+x3
2. Relate acceleration to velocity:
We know that acceleration a can also be expressed as:
a=vdvdx
where v is the velocity of the particle. Therefore, we can set up the equation:
vdvdx=−4x+x3
3. Separate variables and integrate:
Rearranging gives:
vdv=(−4x+x3)dx
Now, we integrate both sides. The left side integrates to:
∫vdv=12v2
The right side integrates as follows:
∫(−4x+x3)dx=−2x2+14x4+C
4. Set up the equation after integration:
After integration, we have:
12v2=−2x2+14x4+C
5. Use initial conditions to find C:
We know that when x=0, v=17m/s:
12(17)2=−2(0)2+14(0)4+C
This simplifies to:
12×289=C⟹C=144.5
6. Substitute C back into the equation:
Now our equation becomes:
12v2=−2x2+14x4+144.5
7. Find the velocity when x=4:
Substitute x=4:
12v2=−2(4)2+14(4)4+144.5
Calculate the right side:
=−2(16)+14(256)+144.5=−32+64+144.5=176.5
So,
12v2=176.5
Multiplying both sides by 2 gives:
v2=353
Therefore, taking the square root:
v=√353≈18.79m/s
Final Answer
The velocity of the particle when x=4 meters is approximately 18.79m/s.
The acceleration a is given by:
a=−4x(−1+14x2)
This can be rewritten as:
a=−4x+x3
We know that acceleration a can also be expressed as:
a=vdvdx
where v is the velocity of the particle. Therefore, we can set up the equation:
vdvdx=−4x+x3
Rearranging gives:
vdv=(−4x+x3)dx
Now, we integrate both sides. The left side integrates to:
∫vdv=12v2
The right side integrates as follows:
∫(−4x+x3)dx=−2x2+14x4+C
After integration, we have:
12v2=−2x2+14x4+C
We know that when x=0, v=17m/s:
12(17)2=−2(0)2+14(0)4+C
This simplifies to:
12×289=C⟹C=144.5
Now our equation becomes:
12v2=−2x2+14x4+144.5
Substitute x=4:
12v2=−2(4)2+14(4)4+144.5
Calculate the right side:
=−2(16)+14(256)+144.5=−32+64+144.5=176.5
So,
12v2=176.5
Multiplying both sides by 2 gives:
v2=353
Therefore, taking the square root:
v=√353≈18.79m/s
The velocity of the particle when x=4 meters is approximately 18.79m/s.
टॉपर्स ने हल किए ये सवाल
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 1
Explore 15 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
समान प्रश्न
If →A=−ˆi+xˆj−3ˆk and →B=2ˆi−ˆk then the value(s) of x for which the dot product of ¯¯¯A & ¯¯¯B is equal to unity :
View SolutionThe x− component of a certain vector in x−y plane is 2 units and y− component is +2√3 units. What is the magnitude of the vector.
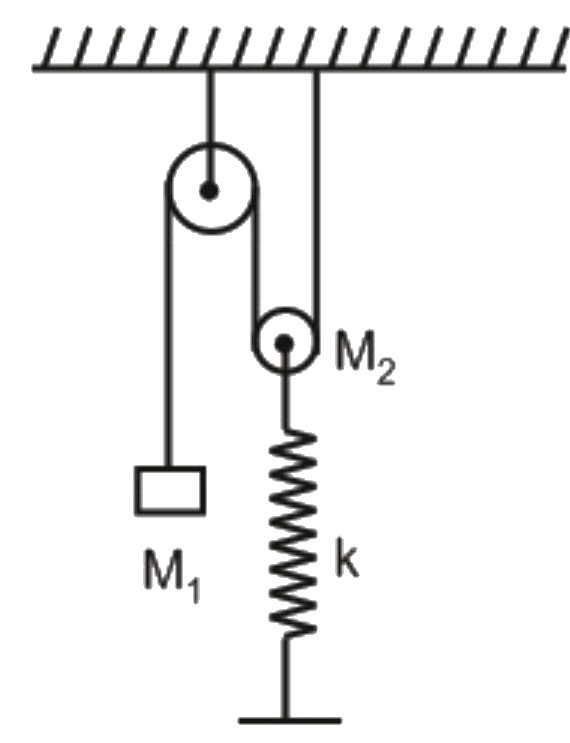
View SolutionA block of mass M1 is constrained to move along with a moveable pulley of mass M2 which is connected to a sprin of force constant k, as shown in the figure. If the mass of the fixed pulley is negligible and friction is absent everywhere, then the period of small oscillations of the system is
View SolutionA time varying voltage is applied across A & B such that voltage across capacitor is given by VC=2sin2t. What is maximum potential difference across the reistance?

View SolutionTwo particles are moving along x-axis. Particle-1 is 40 m behind Particle-2. Particle-1 starts with velocity 12 m//s and acceleration 4 m//s^2 both in positive x-direction. Particle-2 starts with velocity 4 m//s and acceleration 12 m//s^2 also in positive x-direction. Find (a) the time when distance between them is minimum. (b) the minimum distacne between them.
View SolutionThe position of a particle moving on the x-axis is given by x=t^(3)+4t^(2)-2t+5 where x is in meter and t is in seconds (i) the velocity of the particle at t=4 s is 78 m//s (ii) the acceleration of the particle at t=4 s is 32 m//s^(2) (iii) the average velocity during the interval t=0 to t=4 s is 30 m//s (iv) the average acceleration during the interval t=0 to t=4 s is 20 m//s^(2)
View SolutionThe acceleration of a particle moving in straight line is defined by the relation a=−4x(−1+14x2), where a is acceleration in m/s2 and x is position in meter. If velocity v=17m/s when x=0, then the velocity of the particle when x=4 meter is :
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionThe acceleration of a particle is given by the relation as a=−kv5/2 , where is a constant. The particle starts at x=0 with a velocity of 16 m/s, and when x = 6, the velocity is observed to be 4 m/s. Find the velocity of particle when x=5m and the time at which the velocity ofthe particle is 9 m/s.
View SolutionA particle moving along a straight line has a velocity vms−1, when it cleared a distance of x m. These two are connected by the relation v = √49+x. When its velocity is 1ms−1, its acceleration is
View SolutionThe velocity of a particle moving on the x-axis is given by v=x2+x, where x is in m and v in m/s. What is its position (in m) when its acceleration is 30m/s2.
View SolutionA particle starts moving in a straight line from rest with an acceleration ("in"m//s^(2) ) given by : a=12 sqrt x , where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m//s ^(2) is .......m//s
View SolutionThe velocity of a particle defined by the relation v = 8 -0.02x, where v is expressed in m/s and x in meter. Knowing that x = 0 at t = 0, the acceleration at t=0 is
View Solutionसरल रेखा के अनुदिश गतिमान किसी कण का वेग vms−1 है, जब यह x m की दूरी को पार कर लेता है। इन दोनों कोv=√49+x के संबंध के द्वारा जोड़ा जाता है। जब इसका वेग 1ms−1 है, तब इसका त्वरण होगा-
View SolutionThe position of a particle moving along a straight line is given by x =2 - 5t + t ^(3). Find the acceleration of the particle at t =2 s. (x is metere).
View Solution
