Two identical vehicles are moving with same velocity v towards an intersection as shown in figure. If the collision is completely inelastic, then

The correct Answer is:6
The collision is perfectly inelastic
Hence , ∫Ndt=m√2gh
and the linear impulse
∫μNdt=mv
μm√2gh=mv
v=μ√2gh
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
The x− component of a certain vector in x−y plane is 2 units and y− component is +2√3 units. What is the magnitude of the vector.
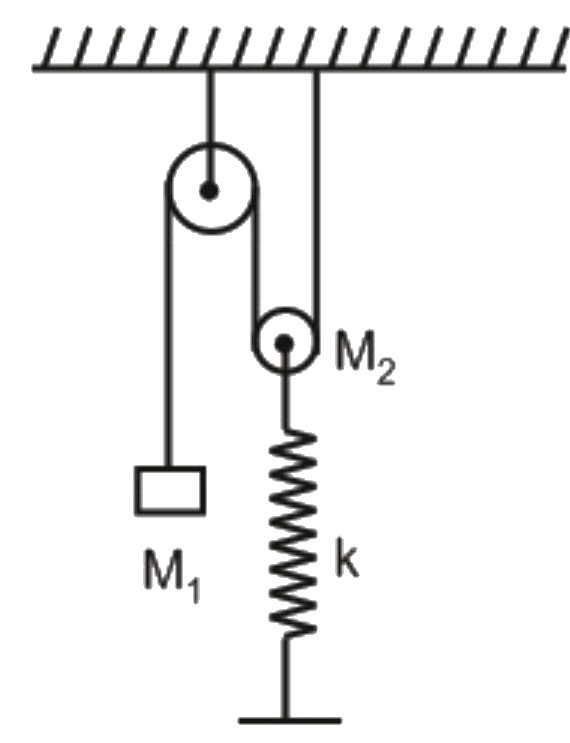
View SolutionA block of mass M1 is constrained to move along with a moveable pulley of mass M2 which is connected to a sprin of force constant k, as shown in the figure. If the mass of the fixed pulley is negligible and friction is absent everywhere, then the period of small oscillations of the system is
View SolutionA time varying voltage is applied across A & B such that voltage across capacitor is given by VC=2sin2t. What is maximum potential difference across the reistance?

View SolutionA ball is moving with velocity 2m//s towards a heavy wall moving towards the ball with speed 1m//s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.
View SolutionTwo identical vehicles are moving with same velocity v towards an intersection as shown in figure. If the collision is completely inelastic, then

View SolutionA ball of mass m moving with velocity V, makes a head on elastic collision with a ball of the same moving with velocity 2V towards it. Taking direction of V as positive velocities of the two balls after collision are.
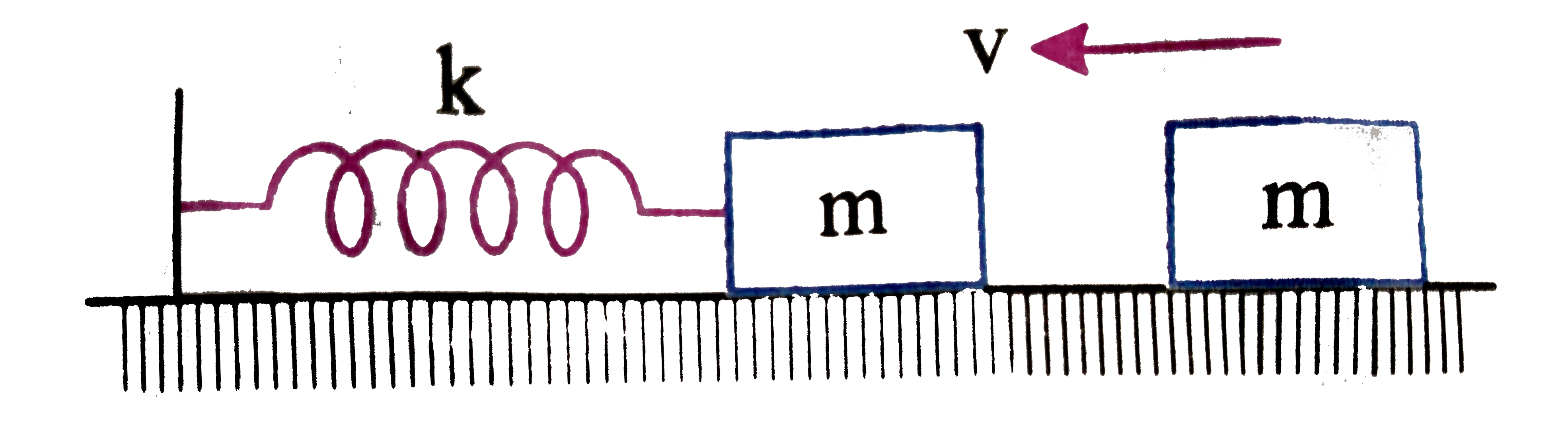
View SolutionThe collision between both blocks shown in figure is completely inelastic. The total energy of oscillation after collision is
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View SolutionTwo identical particles move towards each other with velocity 2 v and v respectively. The velocity of centre of mass is
View SolutionVelocity of the ball A after collision with the ball B as shown in the figure is (Assume perfectly inelastic and head - on collision)
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the combined particle becomes half the initial speed of either particle. The angle between the velocities of the two before collision is
View SolutionTwo identical particles moves towards each other with velocity 2vandv respectively. Two velocity of centre of mass is …………..
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the combined particle becomes half the initial speed of either particle. The angle between the velocities of the two before collision is
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the particles become half the initial speed. The angle between the velocities of the two before collision is:
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the spee of the combined particle becomes half the initial speed of either particle. The angle between the velocities of the two before collision is
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the particles became half the initial speed. The angle between the velocities of the two before collision is
View Solution
