Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0.The top disc is initially at rest. It then falls and sticks to the bottom disc. The change in the rotational kinetic energy of the system is

k∘/6
−(1/2)k∘
−(1/4)k∘
k∘/8
The correct Answer is:B
Step by step video solution for Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity omega_(0) and has rotational kinetic energy K_(0).The top disc is initially at rest. It then falls and sticks to the bottom disc. The change in the rotational kinetic energy of the system is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
The x− component of a certain vector in x−y plane is 2 units and y− component is +2√3 units. What is the magnitude of the vector.
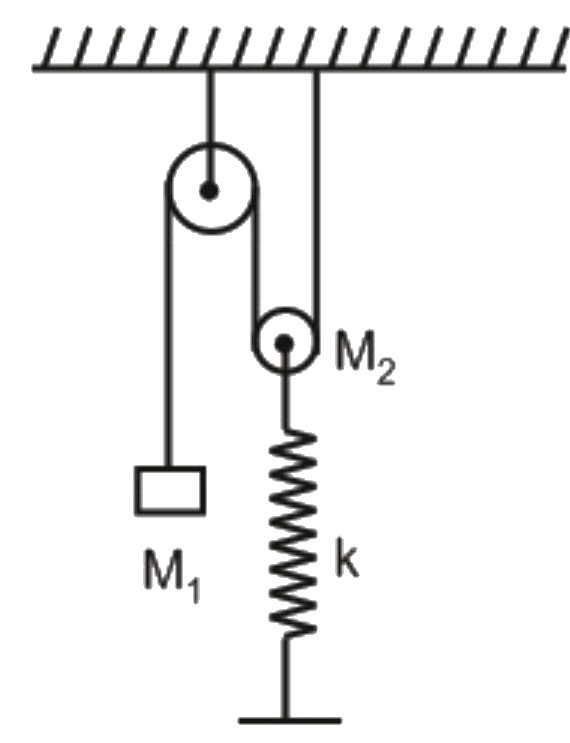
View SolutionA block of mass M1 is constrained to move along with a moveable pulley of mass M2 which is connected to a sprin of force constant k, as shown in the figure. If the mass of the fixed pulley is negligible and friction is absent everywhere, then the period of small oscillations of the system is
View SolutionA time varying voltage is applied across A & B such that voltage across capacitor is given by VC=2sin2t. What is maximum potential difference across the reistance?

View Solution
Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0. Change in the rotational kinetic energy of the system is
View SolutionA circular disc of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular velocity ωi. Another disc of moment of inertia Ib is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed ωf. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionTwo discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω1andω2 are brought into contact face to face with their axes of rotation coincident (i) What is the angular speed of the two-disc system ? (ii) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy ? Take ω1≠ω2.
View Solutionदो चक्रिकाएं जिनके अपने-अपने अक्षों (चक्रिका के अभिलम्बवत तथा चक्रिका के केंद्र से गुजरने वाले) के परितः जड़त्व आघूर्ण I1 तथा I2 हैं और जो ω1 तथा ω2 कोणीय चालों से घूर्णन कर रही हैं को उनके घूर्णन अक्ष सम्पाती करके आमने-सामने लाया जाता है। a. इस दो चक्रिका निकाय की कोणीय चाल क्या है? b. यह दर्शाइए कि इस संयोजित निकाय की गतिज ऊर्जा दोनों चक्रिकाओं की आम्भिक गतिज ऊर्जाओं के योग से कम है। ऊर्जा में हुइ हानि की आप कैसे व्याख्या करेंगे? ω1≠ω2 लीजिए।
View SolutionWhat is the ratio of the rolling kinetic energy and rotational kinetic energy in the motion of a disc ?
View SolutionA disc of moment of inertia la is rotating in a horizontal plane about its symmetry axis with constant angular speed co. Another discinitially at rest of moment of inertia I, is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed The loss of kinetic energy due to friction in this process is,
View SolutionA thin circular disc of mass 12 kg and radius 0.5 m rotates with an angular velocity of 100 rad/s. The rotational kinetic energy of the disc is
View SolutionTwo discs of moments of inertia I_(1) and I_(2) about their respecrtive axes ( normal to the disc and passing through the centre), and rotating with angular speed omega_(1) and omega_(2) are brought into contact face to face with their axes oif rotation coincident. (i) What is the angular speed of the two-disc system? (ii) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energy of the two discs. How do you account for this loss in energy? Take omega_(1) ne omega_(2)
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
View SolutionA disc with moment of inertial I is rotating with some angular speed. Second disc is initially at rest. Now second disc with moment of inertia 3I is placed on first disc and starts rotating. Find loss of kinetic energy in fraction
View SolutionThe moment of inertia of a disc is 100 g . cm^(2) . The disc rotates with an angular velocity 2 rad/s. The rotational kinetic energy of the disc is
View SolutionMoment of inertia of a disc is 100 g.cm2. If the disc rotates with an angular velocity of 2 rad .s−1 the rotational kinetic energy of the disc is
View SolutionTwo discs of moment of inertia I_(1) and I_(2) are rotating separately with angular velocities omega_(1) and omega_(2) respectively about perpendicular axis passing through their centres. If these two rotating discs are connected coaxially then the rotational kinetic energy of the composite system will be
View Solution

