Fundamental frequency of a stretched sonometer wire is f0. When its tension is increased by 96% and length drecreased by 35%, its fundamental frequency becomes η1f0. When its tension is decreased by 36% and its length is increased by 30%, its fundamental frequency becomes η2f0. Then η1η2 is.
4.5
3.5
2
6
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the formula for fundamental frequency
The fundamental frequency f of a stretched sonometer wire is given by the formula:
f=12L√Tμ
where:
- L is the length of the wire,
- T is the tension in the wire,
- μ is the linear mass density of the wire (constant in this case).
Step 2: Analyze the first scenario
In the first scenario, the tension is increased by 96% and the length is decreased by 35%.
- The new tension T1 can be expressed as:
T1=T+0.96T=1.96T
- The new length L1 can be expressed as:
L1=L−0.35L=0.65L
Using these values, we can express the new frequency f1:
f1=12L1√T1μ=12(0.65L)√1.96Tμ=1.961.3⋅12L√Tμ=1.961.3f0
Step 3: Calculate η1
From the above expression, we can find η1:
η1=f1f0=1.961.3=1.961.3≈1.5077
Step 4: Analyze the second scenario
In the second scenario, the tension is decreased by 36% and the length is increased by 30%.
- The new tension T2 can be expressed as:
T2=T−0.36T=0.64T
- The new length L2 can be expressed as:
L2=L+0.3L=1.3L
Using these values, we can express the new frequency f2:
f2=12L2√T2μ=12(1.3L)√0.64Tμ=0.82.6⋅12L√Tμ=0.82.6f0
Step 5: Calculate η2
From the above expression, we can find η2:
η2=f2f0=0.82.6≈0.3077
Step 6: Calculate the ratio η1η2
Now we can find the ratio η1η2:
η1η2=1.50770.3077≈4.89
Conclusion
Thus, the final answer for η1η2 is approximately 4.89.
The fundamental frequency f of a stretched sonometer wire is given by the formula:
f=12L√Tμ
where:
- L is the length of the wire,
- T is the tension in the wire,
- μ is the linear mass density of the wire (constant in this case).
In the first scenario, the tension is increased by 96% and the length is decreased by 35%.
T1=T+0.96T=1.96T
L1=L−0.35L=0.65L
f1=12L1√T1μ=12(0.65L)√1.96Tμ=1.961.3⋅12L√Tμ=1.961.3f0
From the above expression, we can find η1:
η1=f1f0=1.961.3=1.961.3≈1.5077
In the second scenario, the tension is decreased by 36% and the length is increased by 30%.
T2=T−0.36T=0.64T
L2=L+0.3L=1.3L
f2=12L2√T2μ=12(1.3L)√0.64Tμ=0.82.6⋅12L√Tμ=0.82.6f0
From the above expression, we can find η2:
η2=f2f0=0.82.6≈0.3077
Now we can find the ratio η1η2:
η1η2=1.50770.3077≈4.89
Thus, the final answer for η1η2 is approximately 4.89.
टॉपर्स ने हल किए ये सवाल
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 1
Explore 15 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
समान प्रश्न
If →A=−ˆi+xˆj−3ˆk and →B=2ˆi−ˆk then the value(s) of x for which the dot product of ¯¯¯A & ¯¯¯B is equal to unity :
View SolutionThe x− component of a certain vector in x−y plane is 2 units and y− component is +2√3 units. What is the magnitude of the vector.
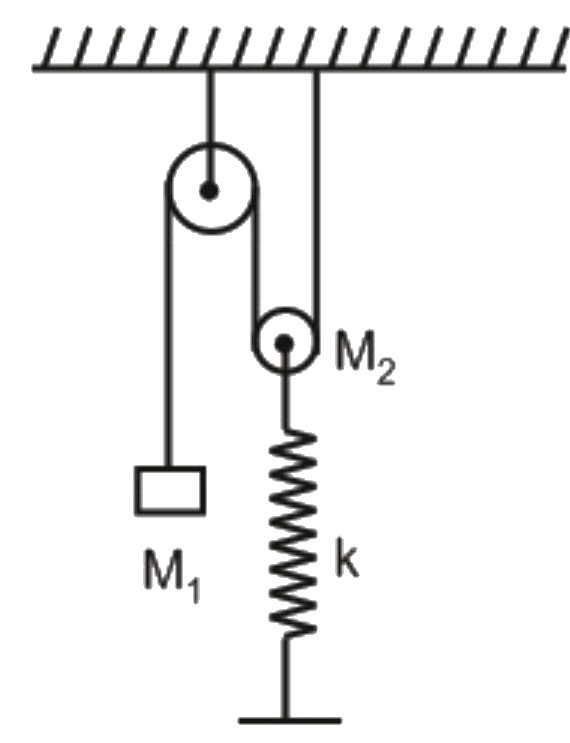
View SolutionA block of mass M1 is constrained to move along with a moveable pulley of mass M2 which is connected to a sprin of force constant k, as shown in the figure. If the mass of the fixed pulley is negligible and friction is absent everywhere, then the period of small oscillations of the system is
View SolutionA time varying voltage is applied across A & B such that voltage across capacitor is given by VC=2sin2t. What is maximum potential difference across the reistance?

View SolutionIf the tension and diameter of a sonometer wire of fundamental frequency n are doubled and density is halved then its fundamental frequency will become
View SolutionIn a Carnot engine when T_(2) = 0^(@)C and T_(1) = 200^(@)C its efficiency is eta_(1) and when T_(1) = 0^(@)C and T_(2) = -200^(@)C . Its efficiency is eta_(2) , then what is eta_(1)//eta_(2) ?
View SolutionThe fundamental frequency of a sonometer wire increases by 5Hz, if its tension is increased by 21% .How will the frequency be affected if the length is increased by 10% /
View SolutionFundamental frequency of a stretched sonometer wire is f0. When its tension is increased by 96% and length drecreased by 35%, its fundamental frequency becomes η1f0. When its tension is decreased by 36% and its length is increased by 30%, its fundamental frequency becomes η2f0. Then η1η2 is.
View SolutionFundamental frequency of a stretched sonometer wire is f_(0) . When its tension is increased by 96% and length decreased by 35%, its fundamental frequency becomes eta_(1) f_(0) . When its tension is decreased by 36% and its length is increased by 30%, its fundamental frequency becomes eta_(2) f_(0) . Find eta_(1)/eta_(2)
View SolutionThe fundatmental frequency of a sonometer wire increases by 6 Hz if its tension is increased by 44% keeping the length constant. Find the change in the fundamental frequency of the sonometer when the length of the wire is increased by 20% keeping the original tension in the wire.
View SolutionThe fundatmental frequency of a sonometer wire increases by 6 Hz if its tension is increased by 44% keeping the length constant. Find the change in the fundamental frequency of the sonometer when the length of the wire is increased by 20% keeping the original tension in the wire.
View SolutionThe fundamental frequency of a stretched string is V_(0) . If the length is reduced by 35% and tension increased by 69% the fundamental frequency will be
View SolutionIf the tension and diameter of a sonometer wire of fundamental frequency n are doubled and density is halved then its fundamental frequency will become
View SolutionIf the tension and diameter of a sonometer wire of fundamental frequency n are doubled and the density halved , then its fundamental frequency will become
View SolutionIf the tension and diameter of a sonometer wire of fundamental frequency vare doubled and density is halved, then its fundamental frequency will become
View SolutionIf the tension and diameter of a sonometer wire of fundamental frequency n is doubled and density is halved, then its fundamental frequency will become .......... .
View Solution
