A 0.60 kg sample of water and a sample of ice are placed in two compartments A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/Kg−K , specific heat of water =4200J/kg−K and latent heat of fusion of ice =3.3×105J/kg.
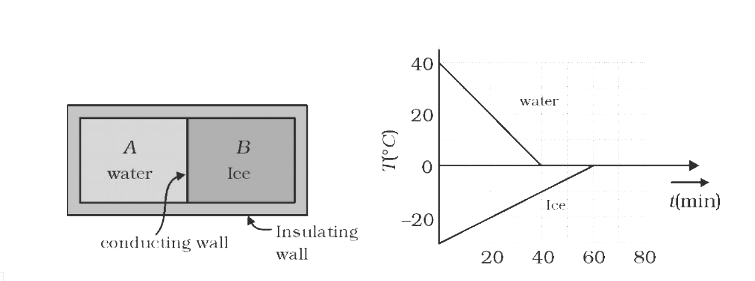
The initial mass of the ice in the container is equal to :
0.36kg
1.2kg
2.4kg
3.6kg
The correct Answer is:C
Sample of ice has been reciving heat at constant rate P from water. Its temperature has increased by 30∘C in time 60min.
Therefore misiΔTiP=60min.
⇒m=(60×60s)×(42W)(2100J/kg).(30∘C)=2.4kg
Topper's Solved these Questions
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-2
1 Video
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercie-3
1 Video
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-1
1 Video
- CALORIMETRYBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise
19 Videos
- CAPACITORBOOK - RESONANCE ENGLISHCHAPTER - CAPACITOREXERCISE - Exercise
34 Videos
Similar Questions
A metal ball of specific gravity 4.5 and specific heat 0.1cal/gm−∘C is placed on a large slab of ice at 0∘C. Half of the ball sinks in the ice. The initial temperature of the ball is:- (Latent heat capacity of ice =80cal/g, specific gravity of ice =0.9)
View SolutionA cube of coefficient of linear expansion α is floating in a bath containing a liquid of coefficient of volume expansion γl. When the temperature is raised by ΔT, the depth upto which the cube is submerged in the liquid remains the same. Find relation between α and γl
View SolutionIn the following equation calculate the value of H.
1kg syeam at 200∘C=H+1kg water at 100∘C(Ssystem= Constant=0.5cal/gm∘C)
View SolutionThe amount of heat required to change the state of 1 kg of substance at constant temperature is called
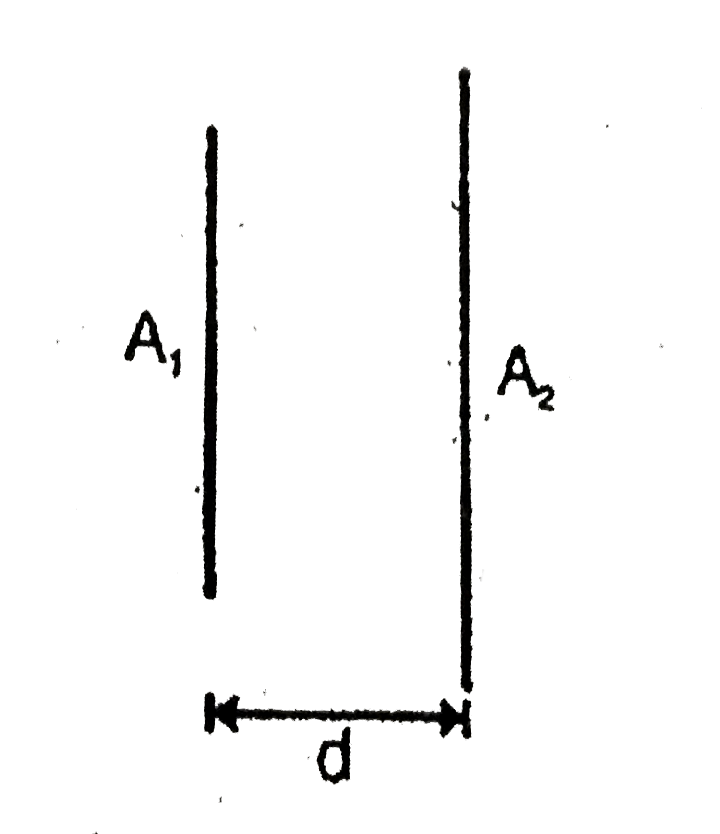
View SolutionThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
View SolutionOn a winter day when the atmospheric temperature drops to -10^(@)C , ice forms on the surface of a lajke. (a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed. (b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches 0^(@)C before the ice starts forming. Density of water =1000kgm^(-3) , latent heat of fusion of ice =3.36xx10^(5)Jkg^(-1) and thermal conductivity of ice =1.7Wm^(-1) ^(@)C^(-1) . Neglect the expension of water on freezing.
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg .
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . Initial mass of the ice in the container equal to
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View SolutionIn an 20 m deep lake, the bottom is at a constant temperature of 4∘C. The air temperature is constant at −10∘C. The thermal conductivity of ice in 4 times that water. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
View Solutionপুকুরের জলের ওপর 5cm পুরু বরফ রয়েছে। বরফের ওপর বায়ুর তাপমাত্রা -10°C। কি হারে প্রতি বর্গ সেন্টিমিটার ক্ষেত্রফলের ভিতর দিয়ে বরফ তাপ পরিবাহিত করবে? বরফের তাপ পরিবাহিতাঙ্ক =5×10−3 CGS unit।
View Solution(a) Two 40g ice cubes are droped into 200g of water in a thermally insulated container. If the water is initially at 25^(@)C , and the ice comes directly from a freezer at - 15^(@)C , what is the final temperature at thermal equilibrium? (b) What is the final temperature if only one ice cube is used ?
View SolutionOn a winter day when the atmospheric temperature drops to −10∘C , ice forms on the surface of a lake. (a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed. (b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches 0∘C before the ice starts forming. Density of water =1000kgm−3 , latent heat of fusion of ice =3.36×105Jkg−1 and thermal conductivity of ice =1.7Wm−1C−1 . Neglect the expansion of water on freezing.
View SolutionA 0.60 kg sample of water ans a sample of ice are placed in two compartments A and B that are separated by a conducting wall in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperatures T of the liquid water and the ice are given in graph as functions of time t. Temperatures of the compartments remain homogeneous during the whole heat transfer process. Given, specific heat of ice = 2100 J/kg-K Specific heat of water = 4200 J/kg-K latent heat of fusion of ice = 3.3 xx 10^(-5) J/kg The value of rate P is
View SolutionA 0.60 kg sample of water ans a sample of ice are placed in two compartments A and B that are separated by a conducting wall in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperatures T of the liquid water and the ice are given in graph as functions of time t. Temperatures of the compartments remain homogeneous during the whole heat transfer process.
Given, specific heat of ice = 2100 J/kg-K
Specific heat of water = 4200 J/kg-K
latent heat of fusion of ice = 3.3×10−5 J/kg
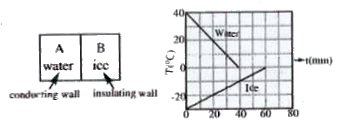
The initial mass of the ice in the container is equal to
View SolutionA 0.60 kg sample of water ans a sample of ice are placed in two compartments A and B that are separated by a conducting wall in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperatures T of the liquid water and the ice are given in graph as functions of time t. Temperatures of the compartments remain homogeneous during the whole heat transfer process. Given, specific heat of ice = 2100 J/kg-K Specific heat of water = 4200 J/kg-K latent heat of fusion of ice = 3.3 xx 10^(-5) J/kg The mass of the ice formed due to conversion from hte water till thermal equilibrium is reached , is equal to
View Solution

