The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

√mkL
kL22M
zero
ML2k
The correct Answer is:A
According to conservation of energy
12kL2=12Mυ2
⇒kL=(Mυ)2M
MkL2=p2 (p=mυ)
∴P=L√MK
Topper's Solved these Questions
Similar Questions
The capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
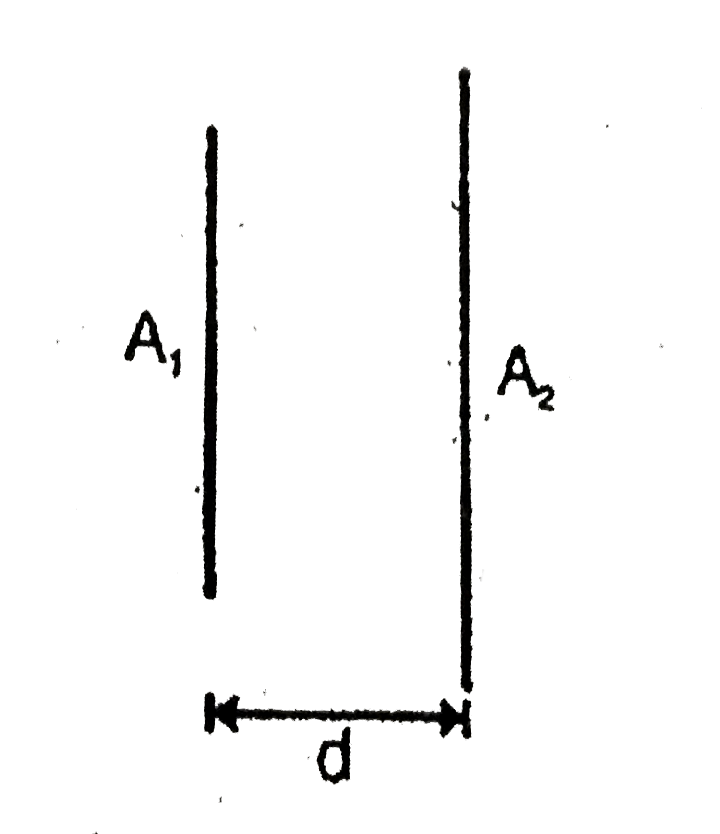
View SolutionA car travels with constant speed on a circular road on level ground. In the figure shown, Fair is the force of air resistance on the car. Which of the other forces best represent the horizontal force of the road on the car's tires ?

View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
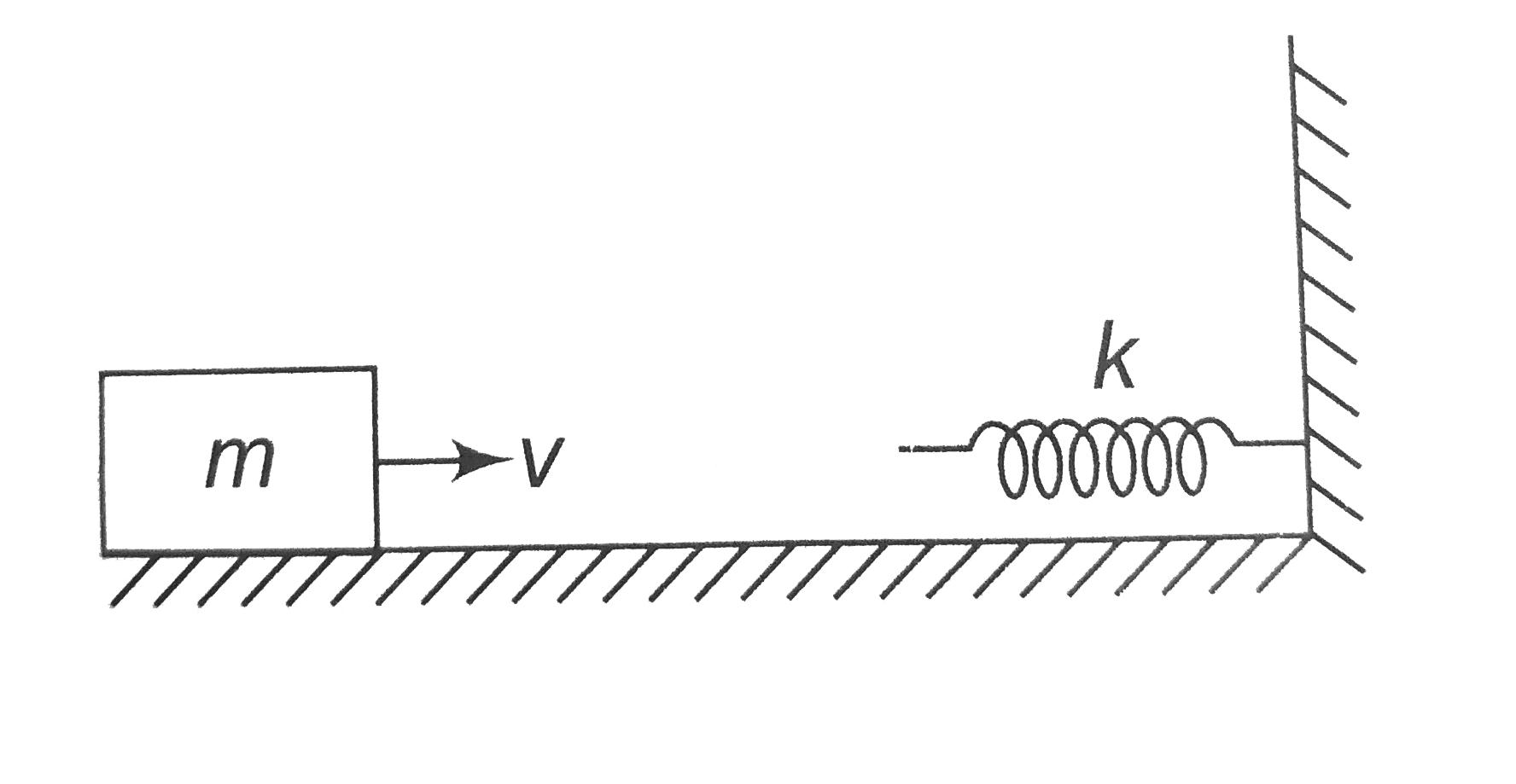
View SolutionA block of mass m moving at a speed v_0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View Solutionचित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके एक घर्षणरहित क्षैतिज सतह पर रखे हैं तथा k स्प्रिंग नियतांक वाले एक स्प्रिंग से जुड़े हैं। प्रारंभ में स्प्रिंग अपनी स्वाभाविक लंबाई में है तथा गुटके स्थिर हैं। अब एक अचर बल F, द्रव्यमान M वाले गुटके पर लगना प्रारंभ करता है। स्प्रिंग की लंबाई में अधिकतम वृद्धि निकालें।
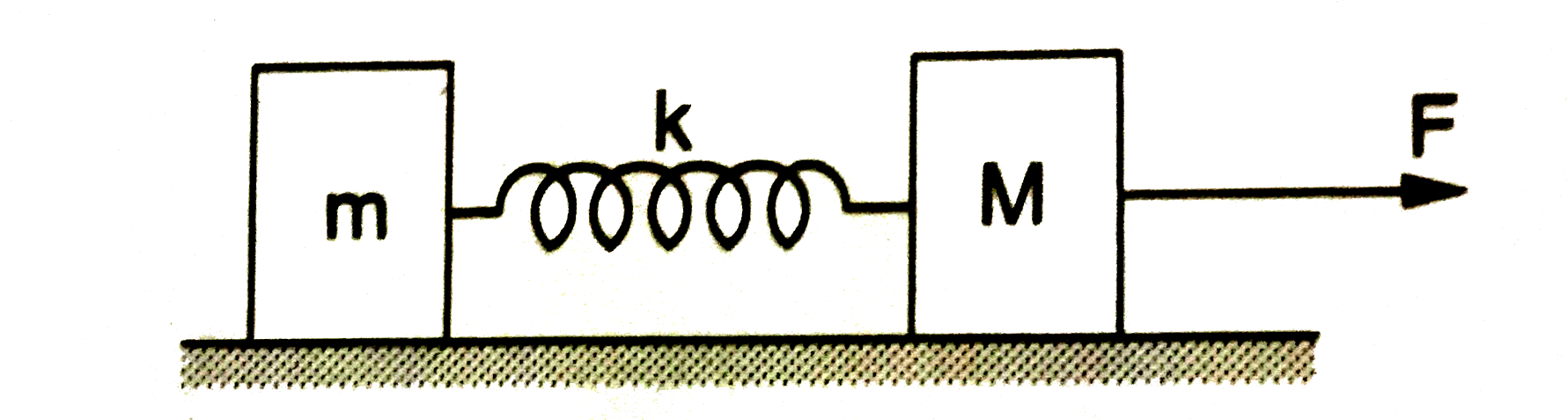
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View Solution15 किग्रा का एक ब्लॉक 0.6 मी/से की चाल से एक घर्षणहीन मेज के क्षैतिज तल पर फिसलता है। यह ब्लॉक एक स्प्रिंग को संकुचित कर एक क्षण के लिए विरामावस्था में आ जाता है । स्प्रिंग में उत्पन्न अधिकतम संकुचन ज्ञात कीजिये। ( स्प्रिंग नियतांक k=1500 न्यूटन/ मी )
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
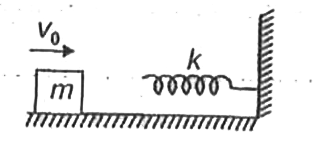
View SolutionA mass m moves with a speed v on a horizontal smooth surface and collides with a nearly massless spring whose spring constant is k. If the mass stops after collision, compute the maximum compression of the spring.
View SolutionA block of mass M moves on a frictionless horizontal surface to make k the segmental constant. The maximum momentum of the block will be after the collision
View Solutionm द्रव्यमान का एक गुटका v चाल से क्षैतिज खुरदुरी सतह पर गतिमान है तथा चित्रानुसार स्प्रिंग नियतांक k वाली क्षैतिज रूप से व्यवस्थित स्प्रिंग से टकराता है। गुटके एवं फर्श के मध्य का घर्षण गुणांकμ है। स्प्रिंग का अधिकतम संपीड़न होगा-

View SolutionM द्रव्यमान का एक गुटका जो घर्षणशील क्षैतिज सतह पर गति कर रहा है K स्प्रिंग नियतांक की एक स्प्रिंग से टकराता है तथा इसे L दूरी संपीडित करता है। संघट्ट के पश्चात गुटके का अधिकतम संवेग है-

View SolutionA block of mass .M. moving on the firctionless , horizontal surface collides with the spring of spring constant .k.. The other end of the spring is rigidly fixed to a vertical wall. If the spring is compressed by L, the maximum momentum of the block after collision is :
View SolutionA block of mass 'M' moving on the firctionless horizontal surface collides with the spring of spring constant 'k'. The other end of the spring is rigidly fixed to a vertical wall. If the spring is comressed by L, the maximum momentum of the block after collision is :
View SolutionA block of mass 'M' moving on the firctionless horizontal surface collides with the spring of spring constant 'k'. The other end of the spring is rigidly fixed to a vertical wall. If the spring is comressed by L, the maximum momentum of the block after collision is :
View Solution
