A string of length 'l' is fixed at both ends. It is vibrating in tis 3rd overtone with maximum amplitude 'a' the amplitude at a distance l3 from one end is
a
0
√3a2
a2
The correct Answer is:C
For a string vibrating in its nth overtone ((n+1)th harmonic)
y=2Asin((n+1)πxL)cosωt
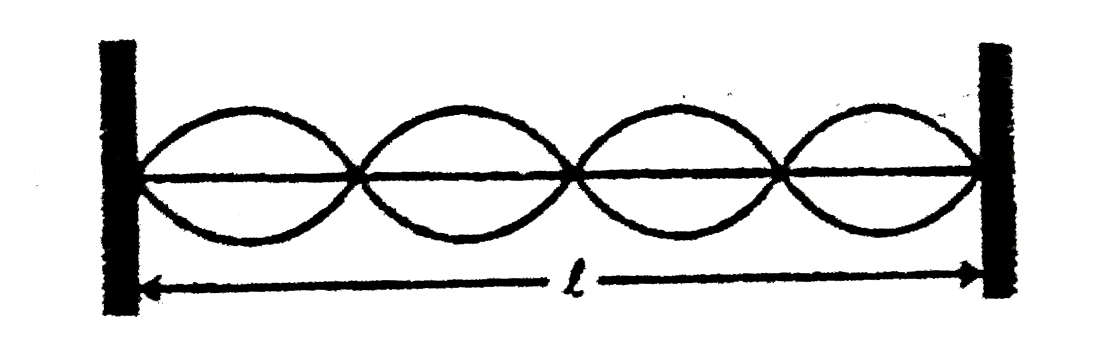
For x=l3,2A=a and n=3, y=[asin(4πl.l3)]cosωt
=asin.4π3cosωt=a(√32)cosωt
i.e., at x=l3 the amplitude is √3a2
Topper's Solved these Questions
Similar Questions
When two tuning forks (fork 1 and fork 2) are sounded simultaneously, 4 beats per second are heard. Now some tape is attached to the prongs of fork 2. When the tuning forks are sounded again, 6 beats per second are heard. If the frequency of fork 1 is 200 Hz, then what was the original frequency of fork 2 ?
View SolutionA long capillary tube of radius r=1mm open at both ends is filled with water and placed vertically. What will be the height (in cm) of the column of water left in the capillary walls is negligible. (surface tension of water is 72dyne/cm and g=1000cm/sec2)
View SolutionWhen the string of a sonometer of length L between the bridges vibrates in the first overtone , the amplitude of vibration is maximum at
View SolutionA string of length 'l' is fixed at both ends. It is vibrating in its 3rd overtone with maximum ampltiude 'a'. The amplitude at a distance l3 from one end is =√pa2. Find p.
View SolutionA string of length l is fixed at both ends and is vibrating in second harmonic. The amplitude at anti-node is 2 mm. The amplitude of a particle at distance l/8 from the fixed end is
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionA string of length 'l' is fixed at both ends. It is vibrating in its 3rd overtone with maximum ampltiude 'a'. The amplitude at a distance l3 from one end is =√pa2. Find p.
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionWhen the string of the sonometer of length l between the bridges vibrates in the first overtone, then the antinode formed from one end of the string will be
View SolutionA string of length L fixed at both ends vibrates in its first overtone. Then the wavelength will be
View SolutionAn open organ pipe has length l .The air in it vibrating in 3^( rd ) overtone with maximum amplitude A.The amplitude at a distance of (l)/(6) from any open end is.
View SolutionAn open organ pipe has length l .The air in it vibrating in 3^( rd ) overtone with maximum amplitude A . The amplitude at a distance of (l)/(16) from any open end is.
View SolutionAn open organ pipe has length l .The air in it vibrating in 3^( rd ) overtone with maximum amplitude A . The amplitude at a distance of (l)/(16) from any open end is
View SolutionA open pipe of length l is vibrating in 3rd overtone with maximum amplitude A. The amplitude at a distance of l16 from any open end is
View SolutionA closed organ pipe has length l . The air in it is vibrating in 3rd overtone with a maximum amplitude of A. Find the amplitude at a distance of l//4 from closed end of the pipe
View SolutionA string of length 'L' is fixed at both ends . It is vibrating in its 3rd overtone with maximum amplitude 'a'. The amplitude at a distance L//3 from one end is
View Solution

