In the above question, the surface charge densities have the correct relation is-
A. σA>σB>σC>σD
B. σA=σB=σC=σD
C. σD>σC>σB>σA
D. σC<σB>σA>σD
σA>σB>σC>σD
σA=σB=σC=σD
σD>σC>σB>σA
σC<σB>σA>σD
The correct Answer is:A
To solve the problem regarding the surface charge densities on different parts of a conductor, we will analyze the relationship based on the geometry of the surfaces involved.
1. Identify the Surfaces:
We have four surfaces on the conductor:
- Surface A: Pointed end
- Surface B: Small semicircle
- Surface C: Long semicircle
- Surface D: Flat surface
2. Understand the Geometry:
- The radius of curvature for each surface is different:
- Surface A (pointed) has the smallest radius of curvature.
- Surface B (small semicircle) has a larger radius than A but smaller than C.
- Surface C (long semicircle) has a larger radius than B.
- Surface D (flat surface) has an infinite radius of curvature.
3. Apply the Concept of Charge Density:
- The surface charge density (σ) is inversely proportional to the radius of curvature (R). This means:
σ∝1R
- Therefore, the smaller the radius of curvature, the higher the surface charge density.
4. Establish the Relationships:
- Since Surface A has the smallest radius, it will have the highest charge density:
σA>σB>σC>σD
- This implies:
- σA (pointed end) > σB (small semicircle) > σC (long semicircle) > σD (flat surface).
5. Select the Correct Option:
- Based on the relationships derived, we can conclude that the correct option is:
- A. σA>σB>σC>σD
Final Answer:
The correct relation of the surface charge densities is:
A. σA>σB>σC>σD
We have four surfaces on the conductor:
- Surface A: Pointed end
- Surface B: Small semicircle
- Surface C: Long semicircle
- Surface D: Flat surface
- The radius of curvature for each surface is different:
- Surface A (pointed) has the smallest radius of curvature.
- Surface B (small semicircle) has a larger radius than A but smaller than C.
- Surface C (long semicircle) has a larger radius than B.
- Surface D (flat surface) has an infinite radius of curvature.
- The surface charge density (σ) is inversely proportional to the radius of curvature (R). This means:
σ∝1R
- Therefore, the smaller the radius of curvature, the higher the surface charge density.
- Since Surface A has the smallest radius, it will have the highest charge density:
σA>σB>σC>σD
- This implies:
- σA (pointed end) > σB (small semicircle) > σC (long semicircle) > σD (flat surface).
- Based on the relationships derived, we can conclude that the correct option is:
- A. σA>σB>σC>σD
The correct relation of the surface charge densities is:
A. σA>σB>σC>σD
Topper's Solved these Questions
Similar Questions
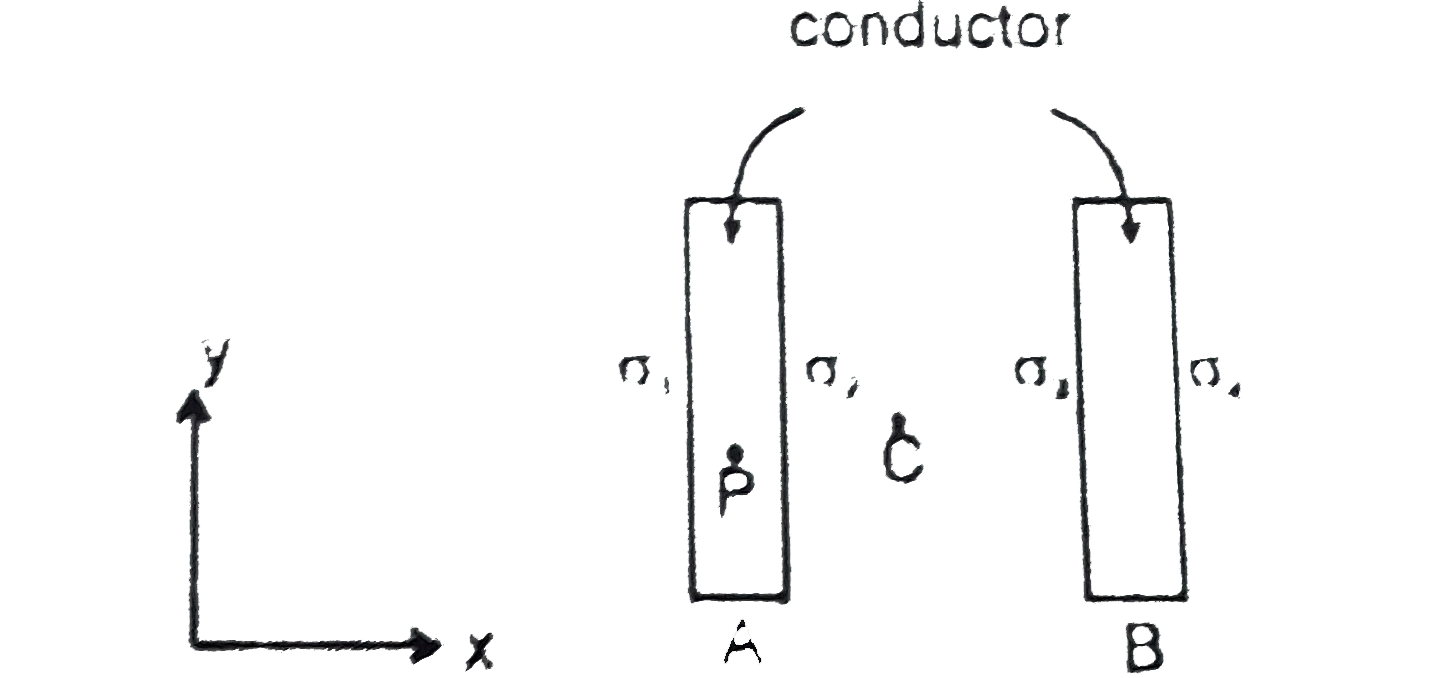
Figure shown two infinitely large conducting plates A and B. If electric field at C due to charge densities σ1,σ2,σ3 and σ40 is Eˆi, find σ2 and σ3 in terms of E. Derive a relation between σ1 and σ4.
View SolutionThe bond order for a species with the configuration σ1s2σ⋆1s2σ2s2σ∗2s2σ2px1 will be
View SolutionIf the standard deviation of a variable X is σ , then standard deviation of variable aX+bc is (a) aσ (b) acσ (c) ∣∣ac∣∣σ (d) aσ+bc
View SolutionIf the standard deviation of a variable X is σ , then standard deviation of variable aX+bc is (a) aσ (b) acσ (c) ∣∣ac∣∣σ (d) aσ+bc
View SolutionTwo paralle plane sheets 1 and 2 carry uniform charge densites σ1andσ2 (see fig. The electric field in the region marked I is (σ1>σ2):

View SolutionIn a sigma bond
View SolutionIf two variates X and Y are connected by the relation Y=aX+bc ,where a,b,c are constants such that ac<0,then (a) σγ=acσX (b) σγ=−acσX (c) σγ=acσX+b (d) none of these
View SolutionTwo parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
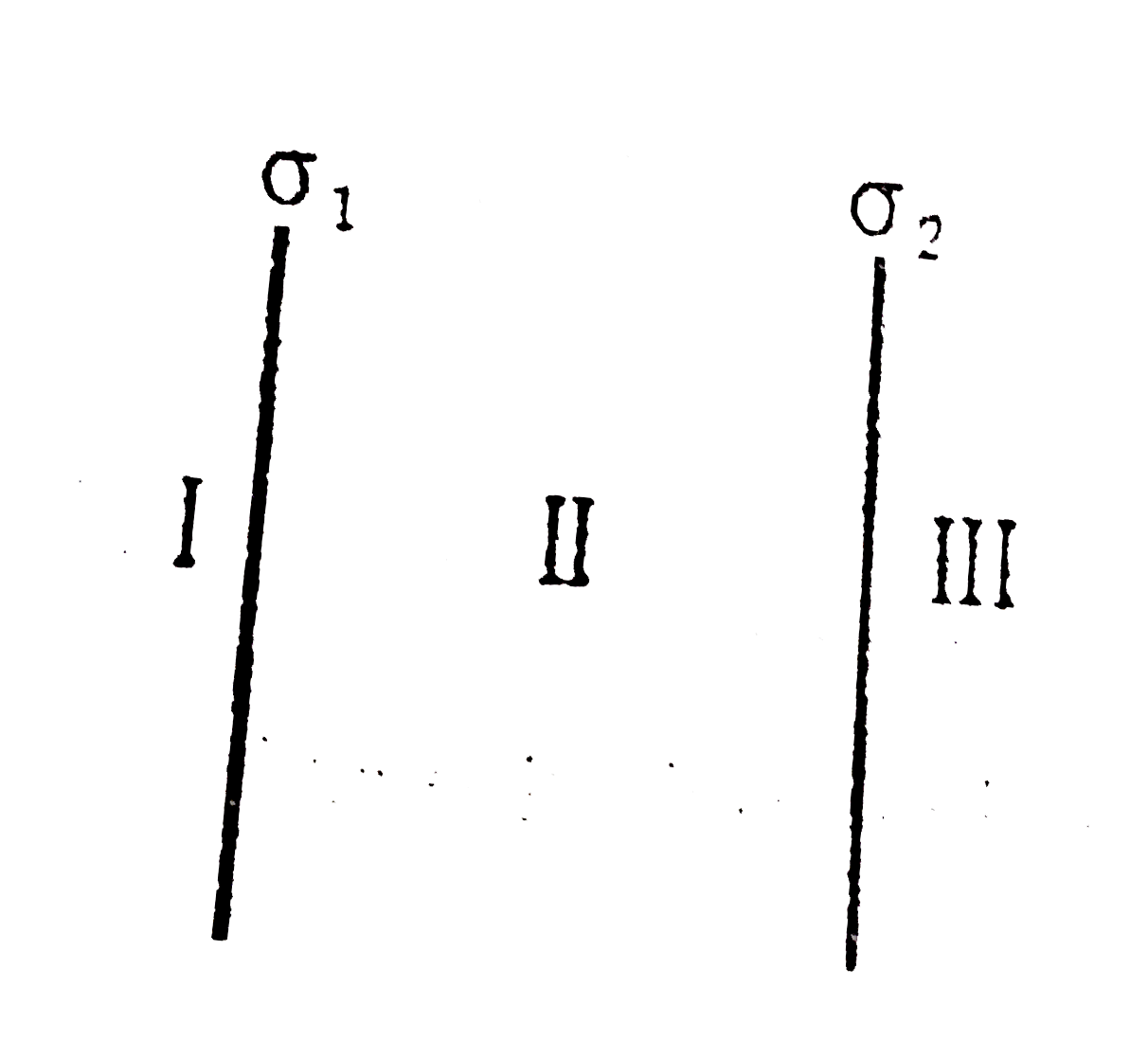
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionThe relation between voltage sensitivity 'σV' and current sensitiviy σi of moving coil galvanometer if its resistance is 'G' is
View SolutionThree infinitely charged sheets are kept parallel to x - y plane having charge densities as shown. Then the value of electric field at 'P' is
A. −4σ∈0ˆk
B. 4σ∈0ˆk
C. −2σ∈0ˆk
D. 2σ∈0ˆk
View Solution

