m1&m2are connected with a light inextensible string with m1 lying on smooth table and m2 hanging as shown in figure m1 is also connected to a light spring which is initially unstretched and the system is released from rest.

system performes SHM with angular frequency given by √k(m1+m2)m1m2
system performs SHM with angular frequency given by √km1+m2
tension in string will be zero when the system is released.
maximum displacement of m1 will be m2gk
The correct Answer is:B
After the system is released, m2 moves down
The extension in the spring becomes
m2gk(m2g=kx0), which is the new equilibrium position of the system,
For small, 'x' : restoring force on the system is
F=kx
⇒a=kxm1+m2 (For (m1+m2+spring ) system)
⇒T=2π√xa=2π√x(m1+m2)kx=2π√m1+m2k
⇒ Angular frequency =ω=2πT=√km1+m2
F.B.D of m1 and m2 just after the system is released
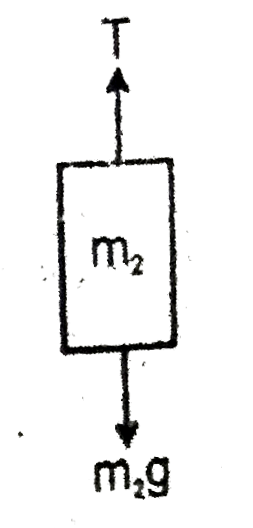

from above : T=m1m2m1+m2g
Hence (3) is incorrect.
After x=m2gk,m1 moves towards right till the total kinetic energy aquired does not converted to potential energy.
Hence (4) is also incorrect.
Hence (2) is the answer.
Topper's Solved these Questions
Similar Questions
The pressure P, volume V and temperature T of a gas in the jar A and the othere gas in the jar B at pressure 2P, volume V/4 and temperature 2T, then the ratio of the number of molecules in the jar A and B will be :
View SolutionIn the situation shown in figure, find the velocity of image.

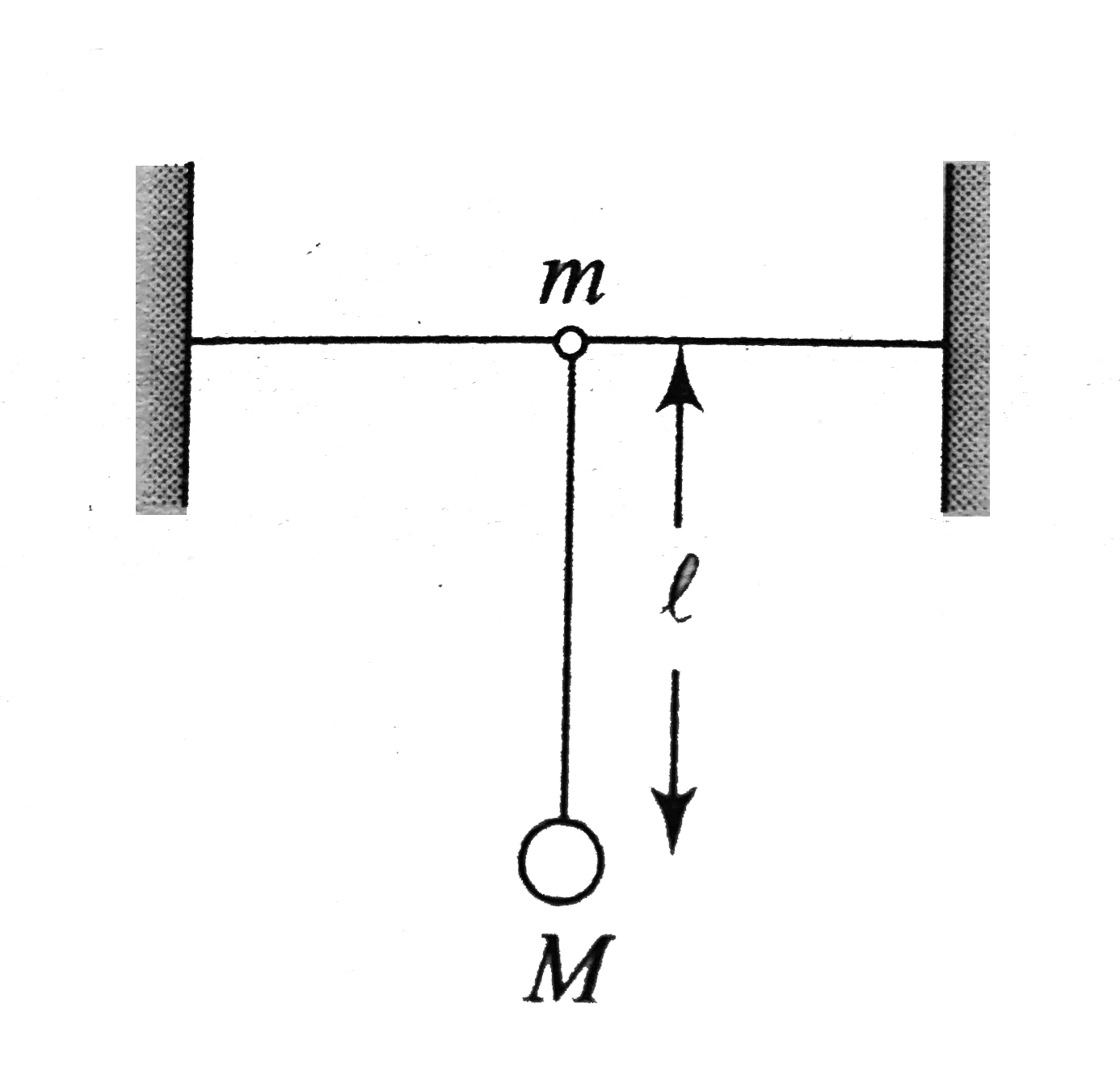
View SolutionA smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
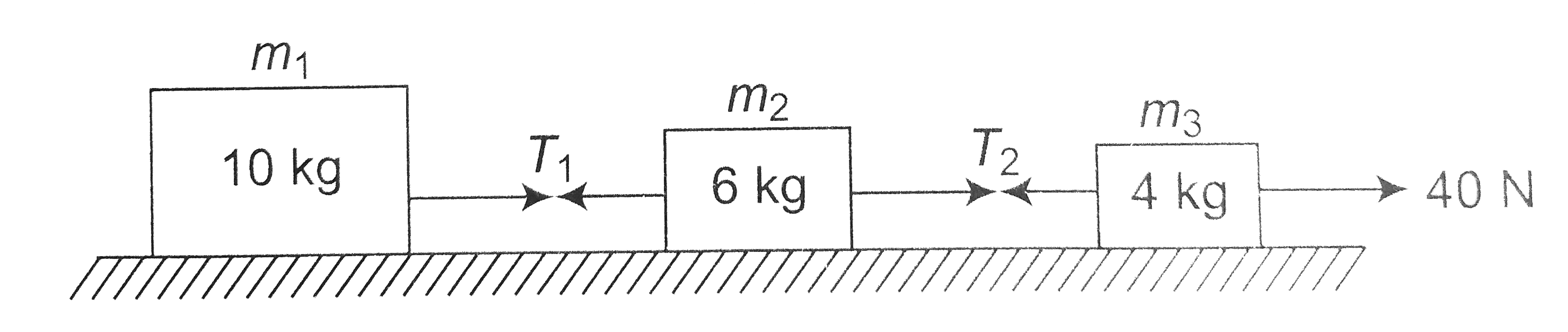
View SolutionThere blocks of masses m1 , m2 and m3 are connected by may less unstretchable strings on a smooth surface. Tension T2 is.
View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
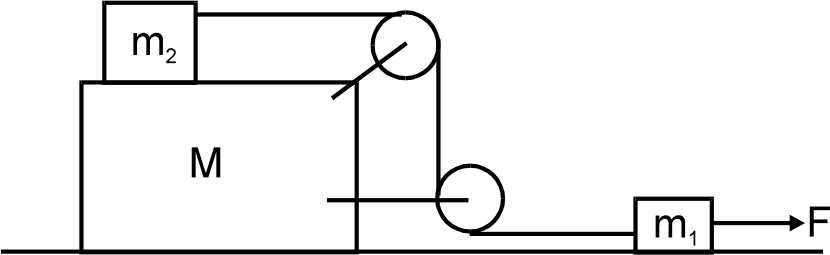
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View SolutionTwo blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :

View Solutionm1 & m2 are connected with a light inextensible string with m1 lying on smooth table and m2 hanging as shown in figure. m1 is also connected to a light spring which is initially unstretched an the system is released from rest.

View SolutionTwo blocks of mass m_(1) and m_(2) , resting on a frictionless table, are connected by a stretched spring and then released -
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m_(1) and m_(2) (vertically).If the acceleration of the system is g/8 then the ratio of masses "m_(1)" to "m_(2)" is "(" take "m_(1)>m_(2)]
View SolutionA block of mass m_(1)=2 kg is kept on a smooth horizontal table. Another block of mass m_(2)=1 kg is connected to m_(1) by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If m_(1)=10kg, m_(2)=6kg and g =10m//s^(2) then what is the acceleration of masses?
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
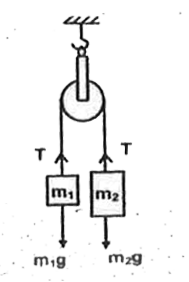
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
View SolutionShown in the figure is a system of three bodies of mass m_(1), m_(2) & m_(3) connected by a single inextensible light string. If all surfaces in contact are smooth & the pulleys P & Q are light, find the tension in the string.
View Solutionm_(1) And m_(2) The two masses are connected by a light thread in such a way that m_(1) Smooth placed on the table and m_(2) Hangs as pictured. m_(1) Is also connected to a light spring which is not pulled at the beginning, then the body is left with a pause then -
View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.

(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View Solution

