A 1.5 kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of an axis is applied to the block. The force is given by →F=(1−x2)ˆiN, where x is in meters and the initial position of the block is x=0 the maximum kinetic energy of the block is 2nJ in between x=0 ad x=2m find the value of n.
To solve the problem, we need to determine the maximum kinetic energy of the block when subjected to the given force. The force acting on the block is →F=(1−x2)^iN.
1. Understanding the Force: The force acting on the block is a function of position x. It is given as F(x)=1−x2. This force will do work on the block as it moves from x=0 to x=2.
2. Work Done by the Force: The work done W by the force as the block moves from position x=0 to x=2 can be calculated using the integral of the force over the distance:
W=∫20F(x)dx=∫20(1−x2)dx
3. Calculating the Integral:
W=∫20(1−x2)dx=(x−x33)20
=(2−233)−(0−0)=2−83=2−2.67=−0.67J
4. Kinetic Energy: According to the work-energy theorem, the work done on the block is equal to the change in kinetic energy. Since the block starts from rest, the initial kinetic energy is 0:
W=ΔKE=KEfinal−KEinitial=KEfinal−0
Therefore, the maximum kinetic energy KEmax is equal to the work done:
KEmax=W=−23J
5. Finding the Value of n: The problem states that the maximum kinetic energy is given by 2nJ. Setting the two expressions for kinetic energy equal gives:
−23=2n
Cross-multiplying gives:
−2n=6⟹n=−3
Final Answer:
The value of n is −3.
W=∫20F(x)dx=∫20(1−x2)dx
W=∫20(1−x2)dx=(x−x33)20
=(2−233)−(0−0)=2−83=2−2.67=−0.67J
W=ΔKE=KEfinal−KEinitial=KEfinal−0
Therefore, the maximum kinetic energy KEmax is equal to the work done:
KEmax=W=−23J
−23=2n
Cross-multiplying gives:
−2n=6⟹n=−3
The value of n is −3.
समान प्रश्न
A 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m is
A.2.33 J B.8.67 J C.5.33 J D.6.67 J
View SolutionA block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
View Solution
ज्ञान जांच
A block of mass 2kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between the block and surface is 0.1. the work done by friction in 10 s is
A200JB−200JC600 JD−600J
A block of mass 2kg si kept at rest at x=0, on a rough horizontal surface with coefficient of a rough horizontal surface with coefficient of friction 0.2. A position dependent horizontal force given by F=x2+2x+5 (where x is in meter and F is in Newton), starts acting on the block at x=0. The kenetic energy of block at x=3 is :
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionBlocks are in contact on a frictionless table. A horizontal force F=3N is applied to one block as shown. The force exerted by the smaller block m2 on block m1 is :
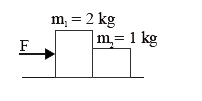
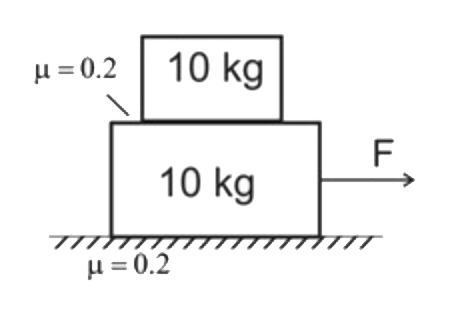
View SolutionInitially, both the blocks are at rest on horizontal surface as shown in the figure. Find the minimum value of force F in (N) so that sliding starts between the blocks (g=10ms−2)
View SolutionTwo blocks of masses 2 kg and 1 kg are in contact with each other on a frictionless table. When a horizontal force of 3.0 N is applied to the block of mass 2 kg the value of the force of contact between the two blocks is:
View SolutionTwo blocks of masses 2 kg and 1 kg are in contact with each other on a frictionless table. When a horizontal force of 3.0 N is applied to the block of mass 2 kg the value of the force of contact between the two blocks is:
View SolutionA block is kept on a rough horizontal surface. A variable horizontal force is acting on the block as shown in the figure. At t=0, block is at rest. Kinectic energy of block at t=5sec will be (g=10m/s2)
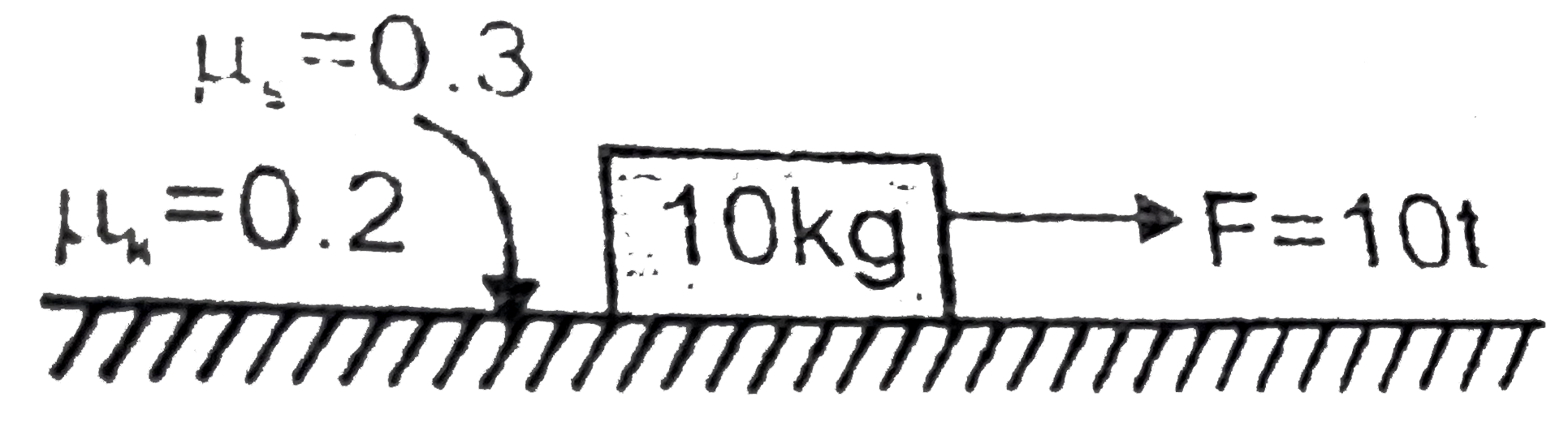
View Solution
