There exist magnetic field →B=yˆi−xˆj in space. What is current (in amperes) crossing through the area enclosed by a circle x2+y2=a2,z=0. Here radius of circle a=1mm
The correct Answer is:5
To solve the problem, we will use Ampere's Circuital Law, which states that the line integral of the magnetic field →B around a closed loop is equal to the permeability of free space μ0 times the total current I enclosed by that loop.
1. Identify the Magnetic Field:
The magnetic field is given as:
→B=y^i−x^j
2. Determine the Area of Interest:
We need to find the current crossing through the area enclosed by the circle defined by:
x2+y2=a2,z=0
where the radius a=1 mm=1×10−3 m.
3. Calculate the Magnitude of the Magnetic Field:
The magnitude of the magnetic field can be expressed as:
|→B|=√y2+(−x)2=√x2+y2
On the circle, since x2+y2=a2:
|→B|=√a2=a
4. Apply Ampere's Circuital Law:
According to Ampere's Circuital Law:
∮→B⋅d→l=μ0Ienc
For a circular path of radius a:
∮→B⋅d→l=|→B|⋅(2πa)
Substitute |→B|=a:
a⋅(2πa)=μ0Ienc
5. Substitute Known Values:
Substituting a=1×10−3 m and μ0=4π×10−7 T m/A:
(1×10−3)⋅(2π⋅1×10−3)=(4π×10−7)Ienc
6. Simplify the Equation:
The left side becomes:
2π×10−6=4π×10−7Ienc
Dividing both sides by 4π×10−7:
Ienc=2π×10−64π×10−7=2×10−64×10−7=5 A
Final Answer:
The current crossing through the area enclosed by the circle is:
Ienc=5 A
The magnetic field is given as:
→B=y^i−x^j
We need to find the current crossing through the area enclosed by the circle defined by:
x2+y2=a2,z=0
where the radius a=1 mm=1×10−3 m.
The magnitude of the magnetic field can be expressed as:
|→B|=√y2+(−x)2=√x2+y2
On the circle, since x2+y2=a2:
|→B|=√a2=a
According to Ampere's Circuital Law:
∮→B⋅d→l=μ0Ienc
For a circular path of radius a:
∮→B⋅d→l=|→B|⋅(2πa)
Substitute |→B|=a:
a⋅(2πa)=μ0Ienc
Substituting a=1×10−3 m and μ0=4π×10−7 T m/A:
(1×10−3)⋅(2π⋅1×10−3)=(4π×10−7)Ienc
The left side becomes:
2π×10−6=4π×10−7Ienc
Dividing both sides by 4π×10−7:
Ienc=2π×10−64π×10−7=2×10−64×10−7=5 A
The current crossing through the area enclosed by the circle is:
Ienc=5 A
Topper's Solved these Questions
Similar Questions
A force F is applied on a block of mass 5kg as shown in figure. Co-efficient of friction between the wall and clock is √32.(g=10m/s2)
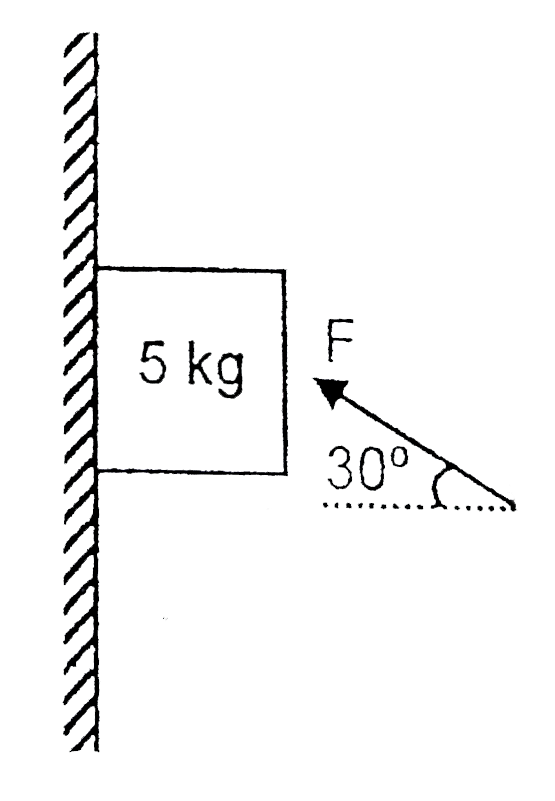
Select correct option(s)
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionFind the values of x, y and z so that the vectors →a=xˆi+2ˆj+zˆkand →b=2ˆi+yˆj+ˆkare equal.
View SolutionIf →a=xˆi+2ˆj− zˆk and →b=3ˆi− yˆj+ˆk are two equal vectors, then write the value of x+y+z.
View SolutionIf →a=xˆi+yˆj+zˆk,→b=yˆi+zˆj+xˆkand→c=zˆi+xˆj+yˆk,then→a×(→b×→c)is (a)parallel to (y−z)ˆi+(z−x)ˆj+(x−y)ˆk (b)orthogonal to ˆi+ˆj+ˆk (c)orthogonal to (y+z)ˆi+(z+x)ˆj+(x+y)ˆk (d)orthogonal to xˆi+yˆj+zˆk
View SolutionFor any vector x, the value of (vec xhat i)^(2)+(vec xhat j)^(2)+(vec xhat k)^(2) is equal to
View SolutionFind the value of x, y and z so that the vectors →a=xˆi+2ˆj+zˆk and →b=2ˆi+yˆj+ˆk are equal.
View SolutionIf →a=xˆi+2ˆj−zˆk and→b=3ˆi−yˆj+ˆk are two equal vectors, then write the value of x+y+z.
View SolutionThere exist magnetic field vec(B)=yhat(i)-xhat(j) in space. What is current (in amperes) crossing through the area enclosed by a circle x^(2)+y^(2)=a^(2),z=0 . Here radius of circle a=1 mm
View SolutionA charged particle with velocity →v=xˆi+yˆj moves in a magnetic field →B=yˆi+xˆj. The magnitude of magnetic force acting on the particle is F. Which one of the following statement(s) is/are correct?
View SolutionA uniform magnetic field exists in the space vecB=B_(1)hati+B_(2)hatj+B_(3)hatk . Find the magnetic flux through an area vecS if the area vecS is in (i) x-y plane (ii) y-z plane (iii) z-x plane
View SolutionIf →a=ht(i)−ˆk,→b=xˆi+ˆj+(1−x)ˆk
→c=yˆi+xˆj+(1+x−y)ˆk.
then →a.(→b×→c) depends on
View SolutionA uniform magnetic field exists in the space vecB=B_1hati+B_2hatj-B_3hatk . Find the magnetic flux through an area vecS if the area vecS is in X-Y plane
View SolutionThe intensity of an electric field depends only on the coordinates x and y as follow vec(E)=(a(xhat(i)+yhat(j)))/(x^(2)+y^(2)) where a is a constant and hat(i) and hat(j) are the unit vectors of the x and y-axes. Find the charge within a sphere of radius R with the centre at the origin
View SolutionCircle x^2+y^2=1 The area of the area enclosed by is
View Solution
