A particle of mass 0.1 kg is executing SHM of amplitude 0.1 m . When the particle passes through the mean position , its KE is 8×10−3 J. Find the equation of motion of the particle if the initial phase of oscillation is 45∘
0.1cos(4t+π4)
0.1sin(4t+π4)
0.4sin(t+π4)
0.2sin(π2+2t)
The correct Answer is:B
From equilibrium
12mω2A2=8×10−3⇒12×0.1×ω2×(0.1)2=8×10−3⇒ω=4
So, equation of SHM is x=Asin(ωt+ϕ)=0.1sin(4t+π4).
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - I
Explore 26 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - I
Explore 25 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 105 Videos
Similar Questions
A block of mass m is resting on a piston as shown in figure which is moving vertically with a SHM of period 1s. The minimum amplitude of motion at which the block and piston separate is :

View SolutionTwo particles A and B are performing SHM along x and y-axis respectively with equal amplitude and frequency of 2cm and 1Hz respectively. Equilibrium positions of the particles A and B are at the coordinates [3cm,0] and (0,4cm) respectively. At t=0,B is at its equilibrium position and moving towards the origin, while A is nearest to the origin and moving away from the origin-
Equation of motion of particle B can be written as-
View SolutionThe equation of a particle executing SHM is x=(5m)sin[(πs−1)t+π6]. Write down the amplitude, initial phase constant, time period and maximum speed.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionA force F is applied on a block of mass 5kg as shown in figure. Co-efficient of friction between the wall and clock is √32.(g=10m/s2)
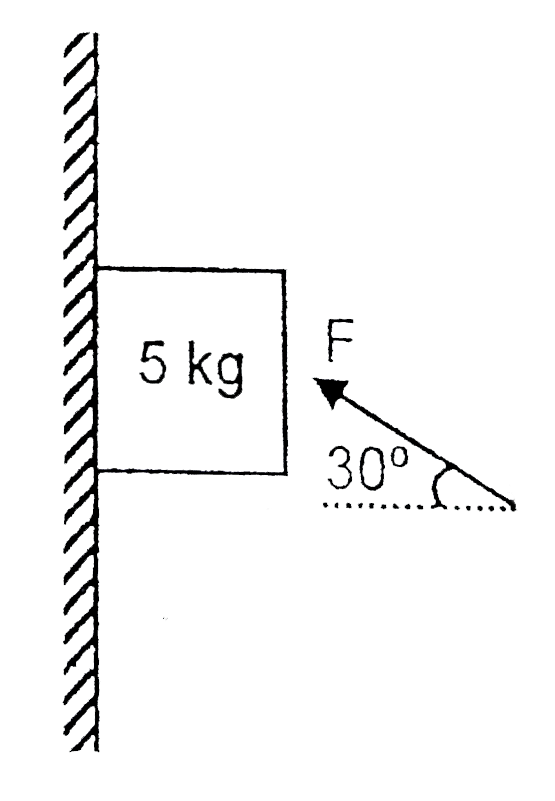
Select correct option(s)
View SolutionA point particle if mass 0.1kg is executing SHM of amplitude 0.1m. When the particle passes through the mean position, its kinetic energy is 8×10−3J. Write down the equation of motion of this particle when the initial phase of oscillation is 45∘.
View SolutionA point particle of mass 0.1kg is executing SHM with amplitude of 0.1m . When the particle passes through the mean position. Its K.E. is 8xx10^(-3)J . Obtain the equation of motion of this particle if the initial phase of oscillation is 45^(@) .
View SolutionA point particle of mass 0.1kg is executing SHM of amplitude 0.1m. When the particle passes through the mean position, its kinetic energy is 8×10−3J. Obtain the equation of motion of this particle if the initial phase of oscillation is 45∘.
View SolutionA point particle of mass 0.1 kg is executing SHM of amplitude 0.1m. When the particle passes through the mean position, its kinetic energy is 8xx10^(-3)J . Obtain the equation of motion of the particle if the initial phase of oscillation is 45^(@)
View SolutionA particle of mass 0.1 kg executes SHM under a for F=(-10x) N. Speed of particle at mean position 6m//s . Then amplitude of oscillations is
View SolutionA particle of mass 0.2 kg is excuting SHM of amplitude 0.2 m. When it passes through the mean position its kinetic energy is 64 xx 10^(-3) J . Obtain the equation of motion of this particle if the initial phase of oscillation is pi//4 .
View Solution0.1 किग्रा द्रव्यमान का एक कण 0.1 मीटर आयाम गति कर रहा है । जब कण साम्य स्थिति से गुजरता है , इसकी गतिज ऊर्जा 8×10−3 जल है । यदि दोलन की प्राम्भिक कला π4 हो , तो कण की गति समीकरण प्राप्त कीजिये ।
View SolutionA particle of mass 0.1 kg is executing simple harmonic motion of amplitude 0.1 m. When the particle passes through the mean position, its kinetic energy is 8xx 10^(-3) J . If the initial phase is 45^@ , the equation of its motion is (Assume, x(t) as the position of the particle at time t . )
View SolutionAmplitude of a particle of mass 0.1 kg executing SHM is 0.1 m. At the mean position its kinetic energy is 8xx10^(-3)J . Find the time period of its vibration.
View SolutionA particle of mass 0.1 kg is executing S.H.M. with amplitude 0.1 m. At the mean position its K.E. is 8×10−3 J. If the intial phase is 45∘. What is the equation of its motion ?
View SolutionA point particle if mass 0.1kg is executing SHM of amplitude 0.1m. When the particle passes through the mean position, its kinetic energy is 8×10−3J. Write down the equation of motion of this particle when the initial phase of oscillation is 45∘.
View Solution
