Two waves travelling in opposite directions produce a standing wave . The individual wave functions are given by y1=4sin(3x−2t) and y2=4sin(3x+2t)cm , where x and y are in cm
To solve the problem of two waves traveling in opposite directions producing a standing wave, we will follow these steps:
Step 1: Write down the wave functions
The individual wave functions are given as:
- y1=4sin(3x−2t)
- y2=4sin(3x+2t)
Step 2: Apply the principle of superposition
According to the principle of superposition, the resultant wave function y can be obtained by adding the two wave functions:
y=y1+y2
Substituting the values of y1 and y2:
y=4sin(3x−2t)+4sin(3x+2t)
Step 3: Factor out the common term
We can factor out the common coefficient:
y=4(sin(3x−2t)+sin(3x+2t))
Step 4: Use the trigonometric identity
Using the trigonometric identity for the sum of sines:
sinA+sinB=2sin(A+B2)cos(A−B2)
Let A=3x−2t and B=3x+2t:
y=4⋅2sin(3x)cos(−2t)
Since cos(−θ)=cos(θ):
y=8sin(3x)cos(2t)
Step 5: Identify the standing wave characteristics
The resultant wave function is:
y=8sin(3x)cos(2t)
This represents a standing wave where:
- The amplitude A=8sin(3x)
- The angular frequency ω=2
Step 6: Determine the position of nodes and antinodes
To find the nodes (where y=0):
8sin(3x)=0⟹sin(3x)=0
This occurs when:
3x=nπ⟹x=nπ3
where n is an integer.
To find the antinodes (where y is maximum):
The maximum value of sin(3x) is 1, which occurs at:
3x=π2+nπ⟹x=π6+nπ3
where n is an integer.
Final Result
The positions of the antinodes are given by:
x=π6,π2,5π6,…
The individual wave functions are given as:
- y1=4sin(3x−2t)
- y2=4sin(3x+2t)
According to the principle of superposition, the resultant wave function y can be obtained by adding the two wave functions:
y=y1+y2
Substituting the values of y1 and y2:
y=4sin(3x−2t)+4sin(3x+2t)
We can factor out the common coefficient:
y=4(sin(3x−2t)+sin(3x+2t))
Using the trigonometric identity for the sum of sines:
sinA+sinB=2sin(A+B2)cos(A−B2)
Let A=3x−2t and B=3x+2t:
y=4⋅2sin(3x)cos(−2t)
Since cos(−θ)=cos(θ):
y=8sin(3x)cos(2t)
The resultant wave function is:
y=8sin(3x)cos(2t)
This represents a standing wave where:
- The amplitude A=8sin(3x)
- The angular frequency ω=2
To find the nodes (where y=0):
8sin(3x)=0⟹sin(3x)=0
This occurs when:
3x=nπ⟹x=nπ3
where n is an integer.
The maximum value of sin(3x) is 1, which occurs at:
3x=π2+nπ⟹x=π6+nπ3
where n is an integer.
The positions of the antinodes are given by:
x=π6,π2,5π6,…
Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Solved Miscellaneous Problems
7 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Board Level Exercise
27 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART II
7 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
7 Videos
Similar Questions
A wave pulse moving along the x axis is represented by the wave funcation
y(x,t)=2(x−3t)2+1
where x and y are measured in cm and t is in seconds.
(i) in which direction is the wave moving ?
(ii) Find speed of the wave.
(iii) Plot the waveform at t=0,t=2s.
View SolutionWhat is a harmonic wave function ?
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionTwo parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I and I, respectively, find the resultant intensity at the focus.
View SolutionThe mathmaticaly form of three travelling waves are given by Y_(1)=(2 cm) sin (3x-6t) Y_(2)=(3 cm) sin (4x-12t) And Y_(3)=94 cm) sin(5x-11t) of these waves,
View SolutionFind the resultant amplitude and the phase difference between the resultant wave and the first wave , in the event the following waves interfere at a point , y_(1) = ( 3 cm) sin omega t , y_(2) = ( 4 cm) sin (omega t + (pi)/( 2)), y_(3) = ( 5 cm ) sin ( omega t + pi)
View SolutionTwo waves travelling in opposite directions produce a standing wave . The individual wave functions are given by y_(1) = 4 sin ( 3x - 2 t) and y_(2) = 4 sin ( 3x + 2 t) cm , where x and y are in cm
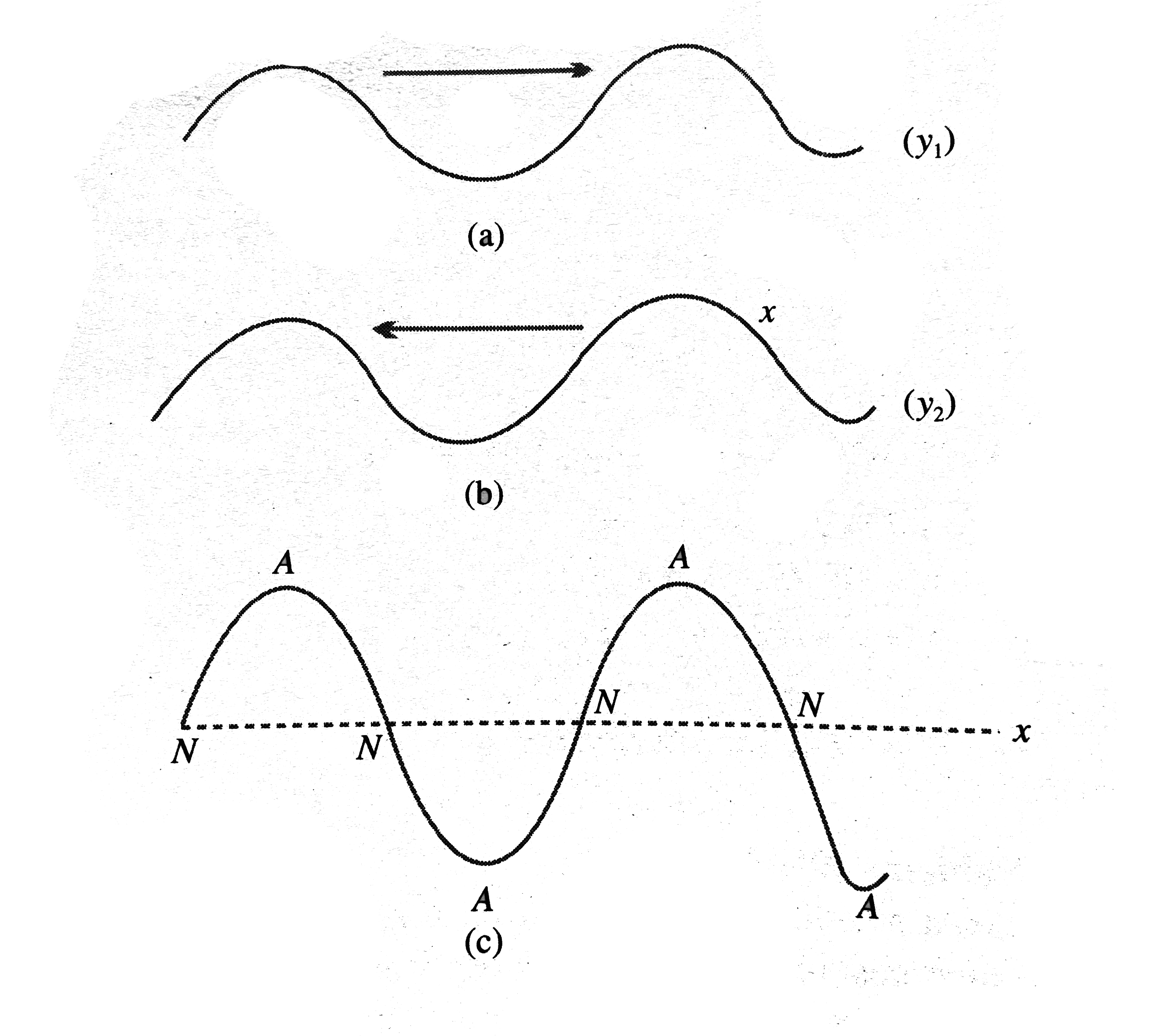
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string
View SolutionTwo wave are represented by equation y_(1) = a sin omega t and y_(2) = a cos omega t the first wave :-
View SolutionStatement-1 : The superposition of the waves y1=Asin(kx−ωt) and y2=3Asin(kx+ωt) is a pure standing wave plus a travelling wave moving in the negative direction along X-axis
Statement-2 : The resultant of y1 & y2 is y=y1+y2=2Asinkxcosωt+2Asin(kx+ωt).
View Solutiony1=asin(ωt−kx) तथा y2=acos(ωt−kx) दो तरंगें दी गई हैं दोनों तरंगों के बीच कलान्तर है
View Solutiony1=4sinωt तथा y2=3sin(ωt+π2) तरंगो के अध्यारोपण से बनने वाली तरंग का परिणामी आयाम होगा
View SolutionThe mathmaticaly form of three travelling waves are given by
Y1=(2cm)sin(3x−6t)
Y2=(3cm)sin(4x−12t)
And Y3=94cm)sin(5x−11t)
of these waves,
View SolutionFind the resultant amplitude and the phase difference between the resultant wave and the first wave , in the event the following waves interfere at a point , y1=(3cm)sinωt,
y2=(4cm)sin(ωt+π2),y3=(5cm)sin(ωt+π)
View SolutionTwo waves travelling in opposite directions produce a standing wave . The individual wave functions are given by y_(1) = 4 sin ( 3x - 2 t) and y_(2) = 4 sin ( 3x + 2 t) cm , where x and y are in cm
View Solution

