Equations of a stationery and a travelling waves are y1=asinkxcosωtandy2=asin(ωt−kx) The phase differences between two between x1=π3k and x2=3π2kareϕ1andϕ2 respectvely for the two waves. The ratio ϕ1ϕ2is
1
5/6
3/4
6/7
The correct Answer is:D
At x1=π3K and x2=3π2K
Nodes are not formed bacause neither x1 nor x2 gives sinkx=0
∴Δx=x2−x1=7π6K
As this Δx between λ and λ2∴ϕ=π
and ϕ2=KΔx=7π6∴ϕ1ϕ2=67
Topper's Solved these Questions
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 2 PART I
Explore 21 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 2 PART II
Explore 19 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 1 PART I
Explore 23 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 3 PART II
Explore 7 Videos
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Advanced Level Problems
Explore 7 Videos
Similar Questions
the same progressive wave is reprsented by two group I and II. Graoup I shows how the displacement 'y' varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curvse m repersents.
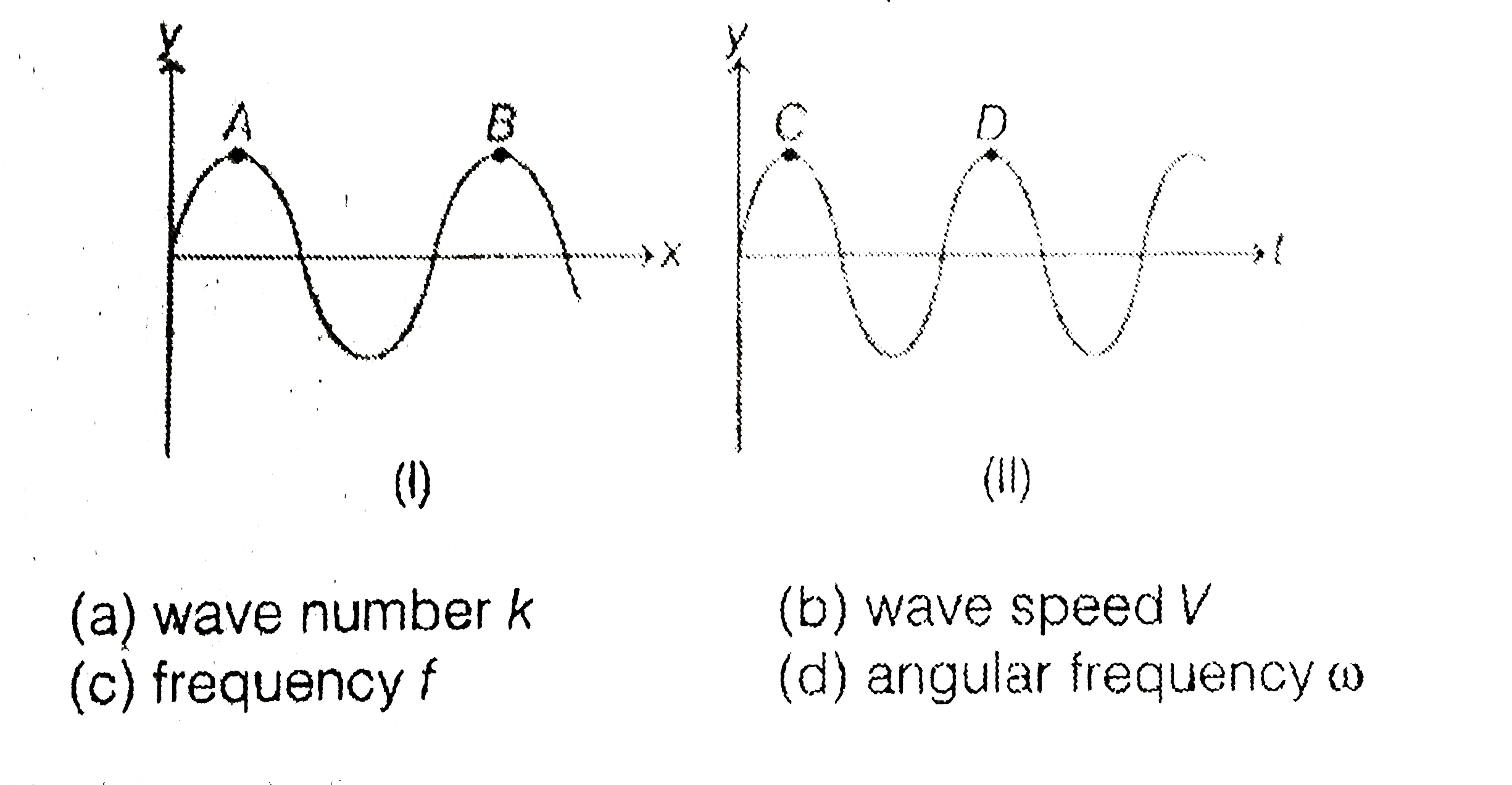
View SolutionA certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View SolutionConsider the wave y=(5mm)sin[1cm−1x−(60s−1)t]. Find (a) the amplitude, (b) the angular wave number, ( c ) the wavelength, (d) the frequency, (e) the time period and (f) the wave velocity.
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionTwo parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I and I, respectively, find the resultant intensity at the focus.
View SolutionAssertion: Two equations of wave are y_(1)=A sin(omegat - kx) and y_(2) A sin(kx - omegat) . These two waves have a phase difference of pi . Reason: They are travelling in opposite directions.
View SolutionEquations of a stationary and a travelling waves are as follows y1=sinkxcosωt and y2=asin(ωt−kx). The phase difference between two points x1=π/3k and x2=3π/2kisϕ1 in the standing wave (y1) and is ϕ2 in the travelling wave (y2) then ratio ϕ1/ϕ2 is
View SolutionThe equation of a travelling and stationary waves are y1=asin(ωt−kx) and y2=asinkxcosωt. The phase difference between two points x1=π4k and 4π3k are ϕ1 and ϕ2 respectively for two waves, where k is the wave number. The ratio ϕ1/ϕ2
View SolutionEquation for two waves is given as y_(1)=asin(omegat+phi_(1)), y_(2)=asin(omegat+phi_(2)) . If ampitude and time period of resultant wave does not change, then calculate (phi_(1)-phi_(2)) .
View SolutionEquations of a stationery and a travelling waves are y_(1)=a sin kx cos omegat and y_(2)=a sin (omegat-kx) The phase differences between two between x_(1)=(pi)/(3k) and x_(2)=(3pi)/(2k) are phi_(1) and phi_(2) respectvely for the two waves. The ratio (phi_(1))/(phi_(2)) is
View SolutionTwo waves are given by y1=asin(ωt−kx) and y2=acos(ωt−kx). The phase difference between the two waves is -
View SolutionFour light sources produce the following four waves
(i) y1=asin(ωt+ϕ1)
(ii) y2=asin2ωt
(iii) y3=a‘sin(ωt+ϕ2)
(iv) y1=asin(ωt+ϕ1)
Superposition of which two waves give rise to interference?
View Solutionप्रगामी तरंगो के समीकरण है -
y1=asin(ωt+ϕ1),y2=asin(ωt+ϕ2)
यदि परिणामी तरंग के आयाम तथा आवर्तकाल वही है जो दोनों तरंगो के है तो (ϕ1−ϕ2) का मान होगा -
View SolutionEquations a stationary and a travelling waves are as. follows y1=asinkxωt and y2=asin(wt−kx) . The phase difference between two pojnt x1=π3k and x2=3π2k are ϕ1 and ϕ2 respectively for the two waves. The ratio ϕ1ϕ2 is:
View SolutionFour light sources produce the following four waves
(i) y1=asin(ωt+ϕ1)
(ii) y2=asin2ωt
(iii) y3=a‘sin(ωt+ϕ2)
(iv) y1=asin(ωt+ϕ1)
Superposition of which two waves give rise to interference?
View SolutionAssertion: Two equations of wave are y_(1)=A sin(omegat - kx) and y_(2) A sin(kx - omegat) . These two waves have a phase difference of pi . Reason: They are travelling in opposite directions.
View Solution
