A wave travels on a light string. The equation of the waves is y=Asin(kx−ωt+30∘). It is reflected from a heavy string tied to an end of the light string at x = 0. If 64% of the incident energy is reflected, then the equation of the reflected wave is
Y=0.8Asin(kx−ωt+30∘+180∘)
Y=0.8Asin(kx+ωt+30∘+180∘)
Y=0.8Asin(kx+ωt−30∘)
Y=0.8Asin(kx+ωt+30∘)
The correct Answer is:C
Step by step video solution for A wave travels on a light string. The equation of the waves is y= A sin (kx - omegat + 30^@). It is reflected from a heavy string tied to an end of the light string at x = 0. If 64% of the incident energy is reflected, then the equation of the reflected wave is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 2 PART II
Explore 19 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 2 PART III
Explore 15 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 1 PART II
Explore 31 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 3 PART II
Explore 7 Videos
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Advanced Level Problems
Explore 7 Videos
Similar Questions
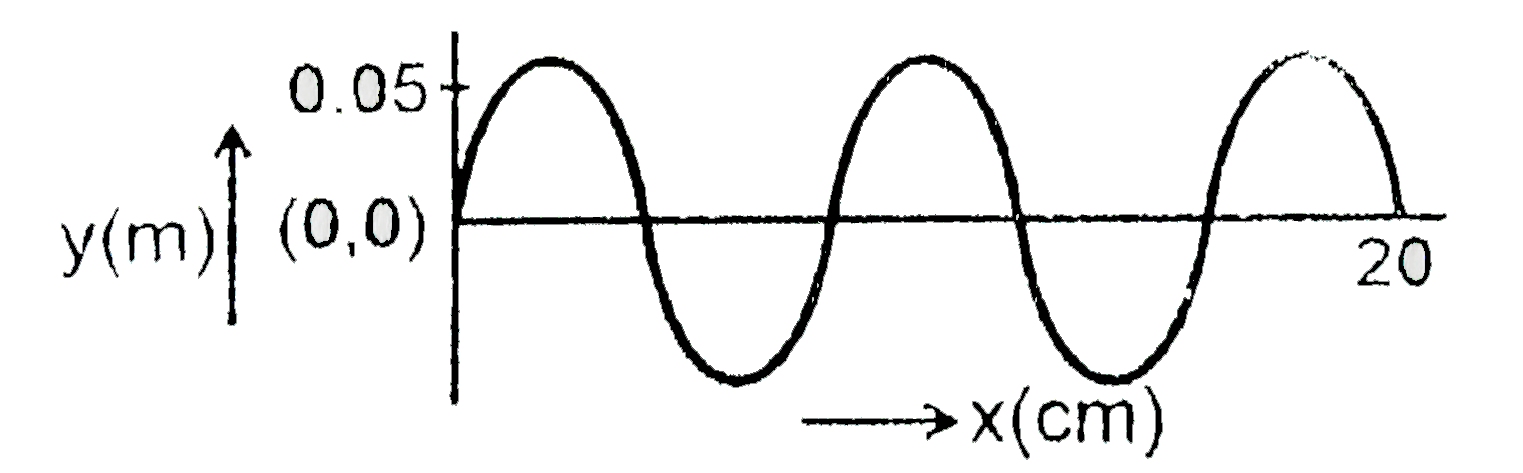
A certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View SolutionThe plane wave represented by an eqution of the form y = f(x-vt) implies the propagation along the positive x-axis without chang of shape with constant velocity v. Then
View SolutionFor the wave shown in figure, the equation for the wave, travelling along +x acis with velocity 350ms−1 when its position at t=0 is as shown
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionTwo parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I and I, respectively, find the resultant intensity at the focus.
View SolutionA wave y = a sin (omegat - kx) on a string meets with another wave producing a node at x = 0 . Then the equation of the unknown wave is
View SolutionA wave travels on a light string. The equation of the waves is y=Asin(kx−ωt+30∘). It is reflected from a heavy string tied to an end of the light string at x = 0. If 64% of the incident energy is reflected, then the equation of the reflected wave is
View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string . The juction of the strings is at x=0. The equation of the reflected wave is
View SolutionA travelling wave y=A sin (kx- omega t +theta ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A . The junction of the strings is at x=0 . The equation fo the refelcted wave is :
View SolutionA wave travels on a light string. The equation of the wave is Y=Asin(kx−ωt+30∘+180∘). It is relected from a heavy string tied to an end of the light string at x=0. If 64% of the incident energy is reflected the equation of the reflected wave is
View SolutionThe sinusoidal wave
y(x,t)=ymsin(kx−ωt)
is incident on the fixed end of a string at x=L. The reflected wave is given by :-
View SolutionA wave on a stretched string is reflected from a fixed end P of the string. The phase difference, at P, between the incident and reflected waves is
View SolutionSpeed of transverse wave on string | Intensity of string wave | Interference of waves travelling in same direction | Standing wave: nodes,antinodes | Reflection and transmission of string wave
View SolutionIntensity and interference of string wave | Reflection and transmission of string waves | Mechanical & non mechanical wave | String wave equation of wave | Condition for valid wave equation
View SolutionA sound wave y= A_0 sin (omegat-kx) is reflected from a rigid wall with 64% of its ampltitude. The equation of the reflected wave is
View SolutionA wave y=asin(ωt−kx) on a string meets with another wave producing a node at x=0. Then the equation of the unknown wave is
View Solution
