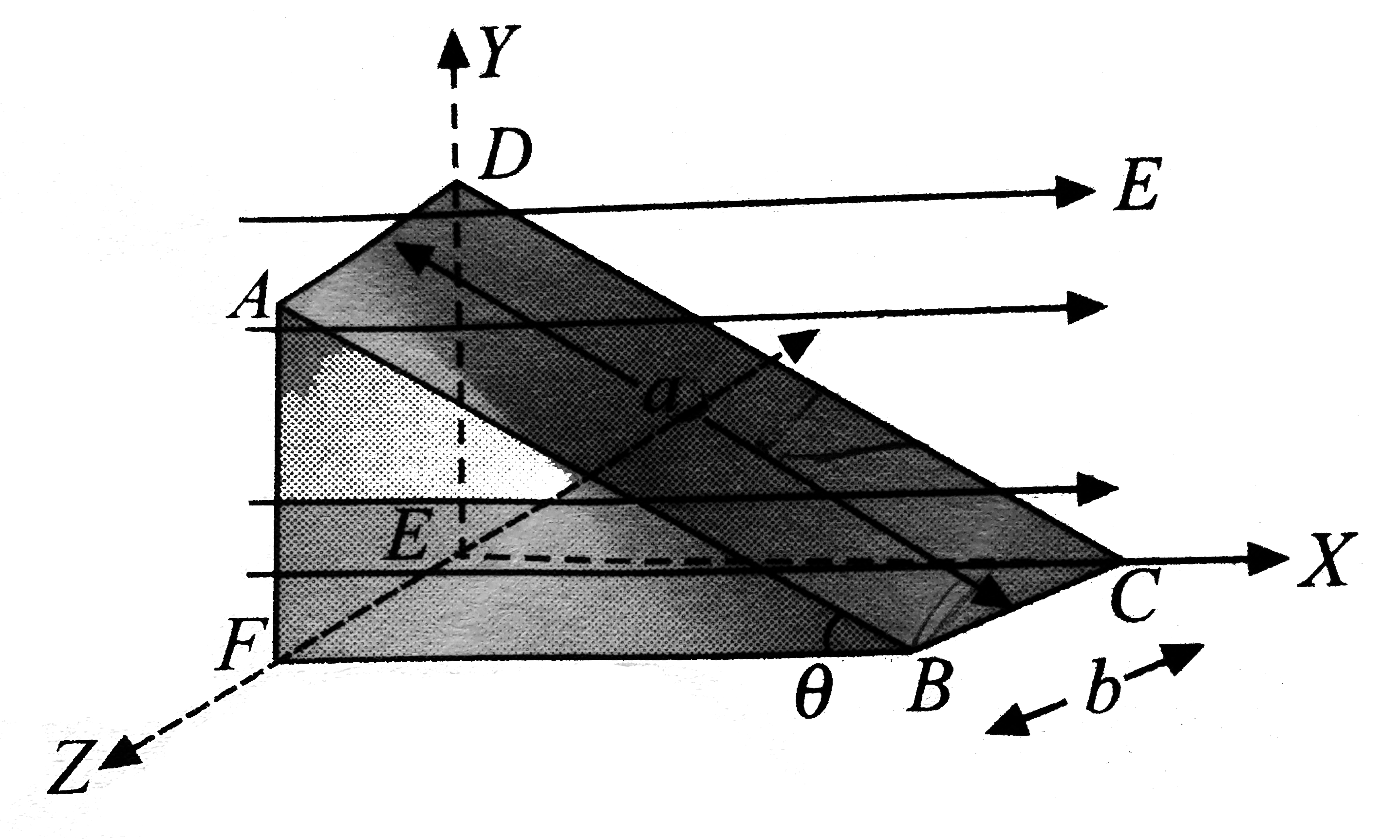
Find r,r',eandδ for the case shown in figure

Here θ=180∘−75∘=105∘
sin45∘=√2sinr
sin45∘=√2sinr
∴r=sin−1(1)2=30∘
r'=180∘−(r+θ)
=180∘−30∘−105∘=45∘
sine=√2sinr'
∴sine=√2×sin5∘=1
∴e=90∘
So, δ=i+e−A=45∘+90∘=6∘

Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1
141 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
33 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
In the L-C-R circuit as shown in figure,
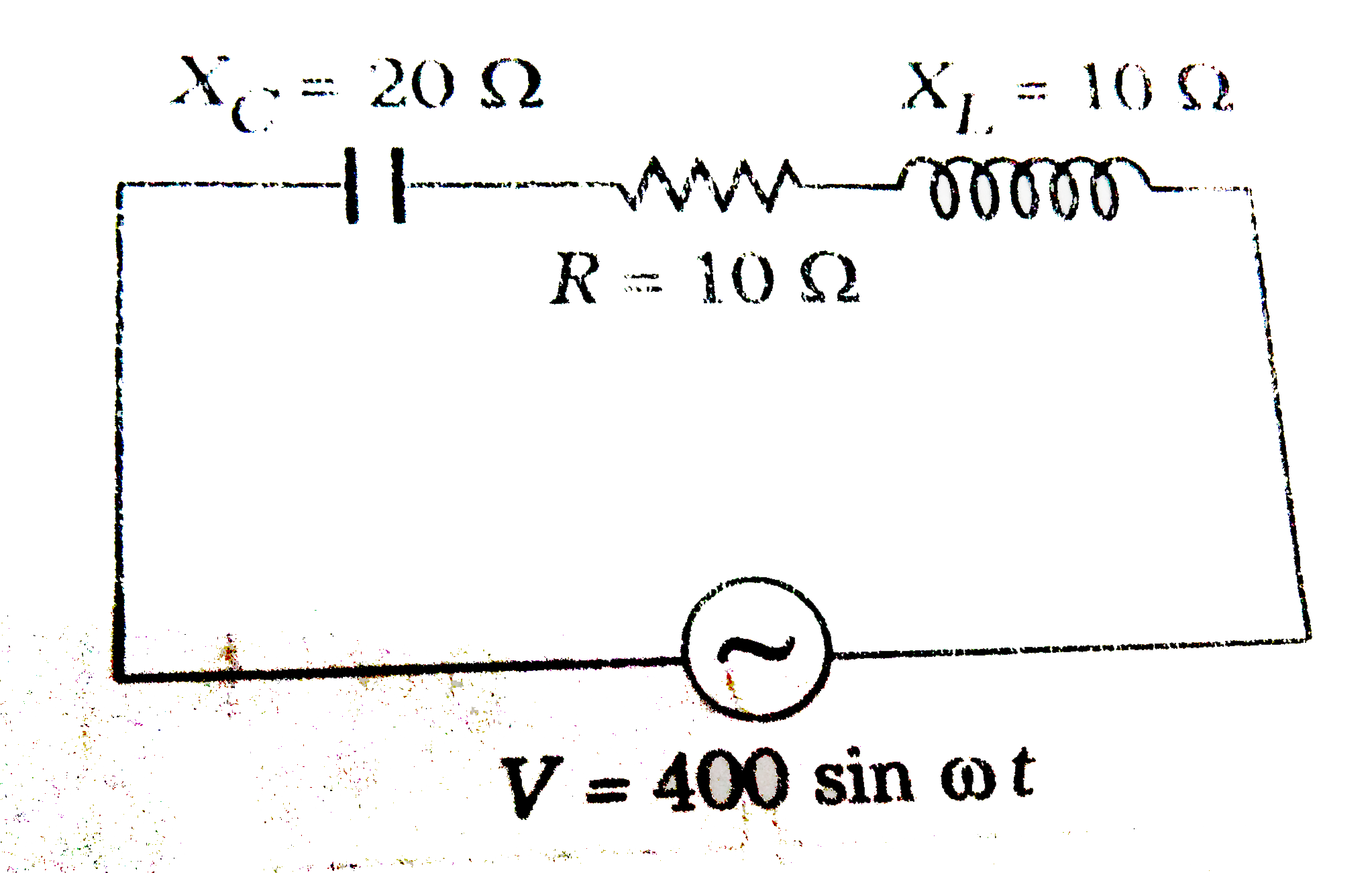
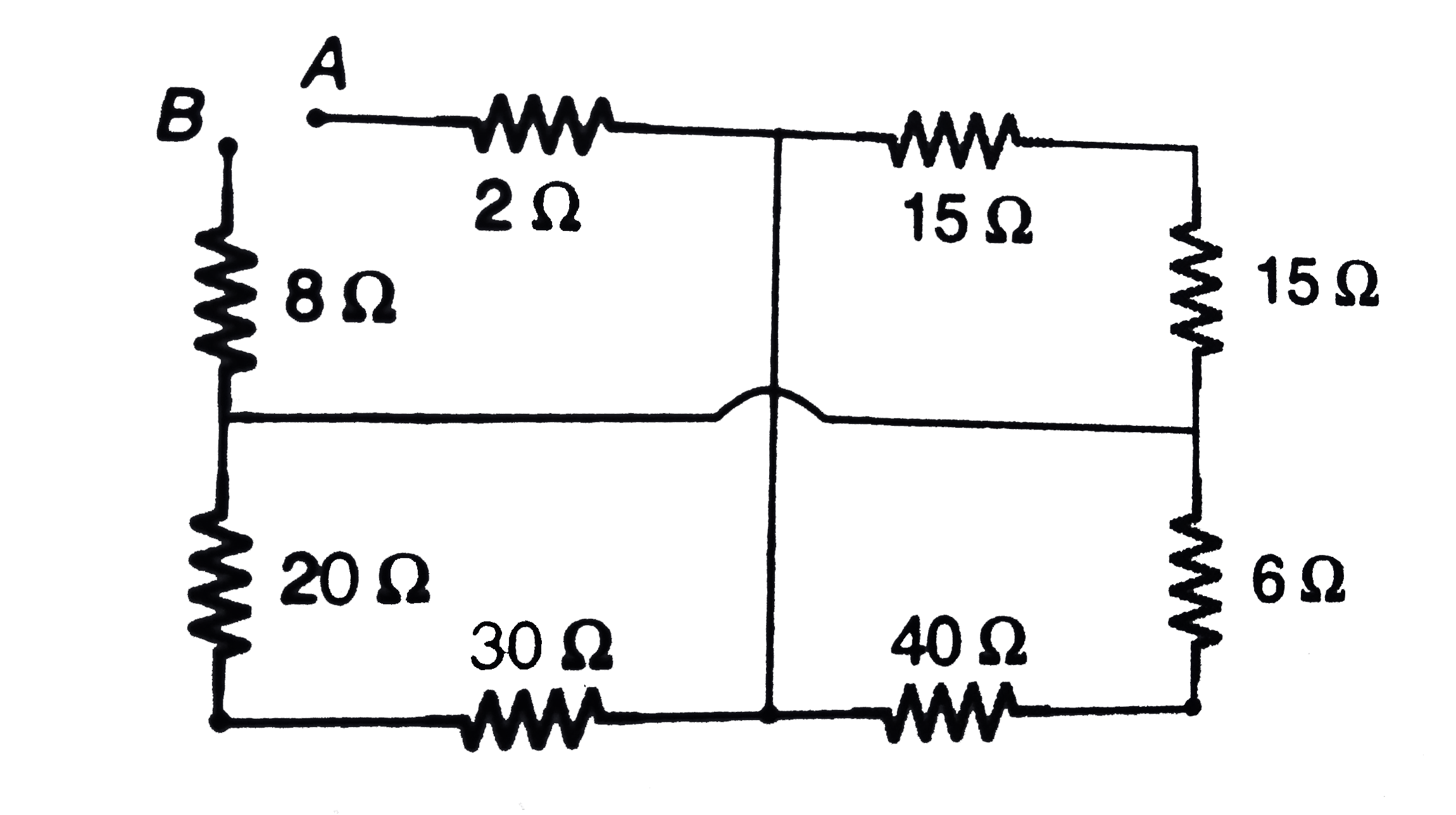
View SolutionFind RAB in the circuit shown in figure.
View SolutionA cell of emf E having an internal resistance R varies with R as shown in figure by the curve

View SolutionThree charges are arranged on the vertices of an equilateral triangle as shown in figure (29.E6) find the dipole moment of the combination.

View SolutionFind the equivalent resistances between the points a and c of the network shown in figure. Each resistance is equal to r.
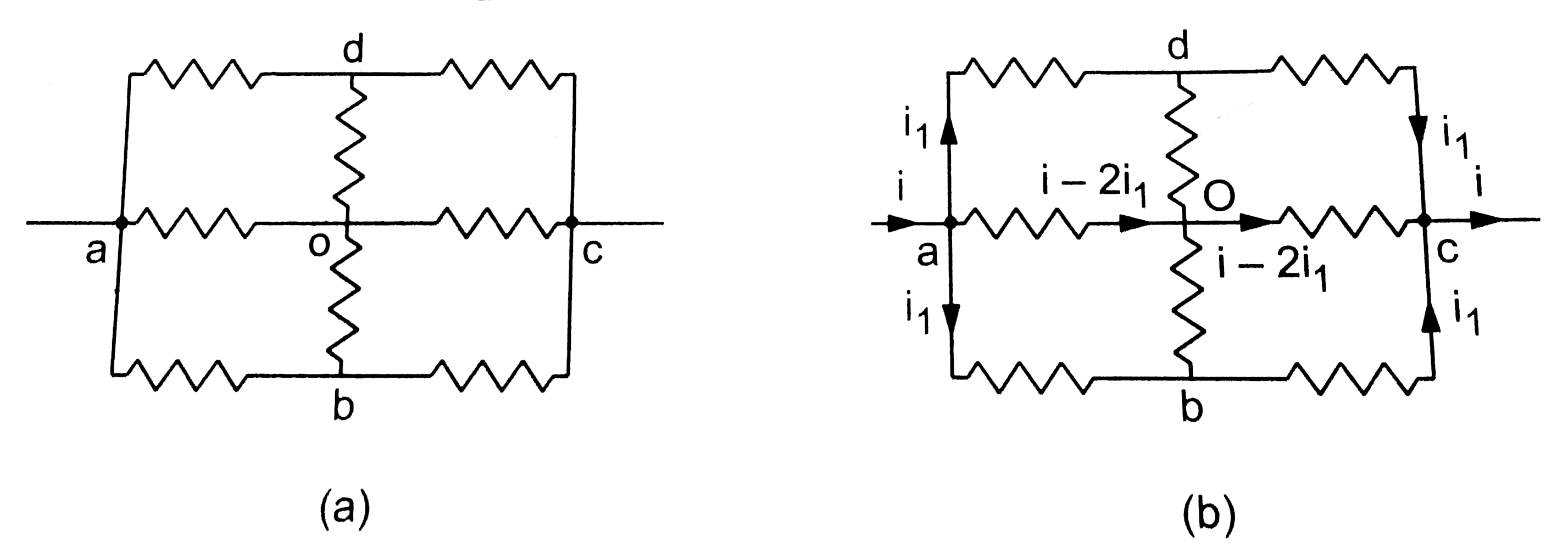
View SolutionA hemispherical surface of radius R is kept in a uniform electric field E as shown in figure. The flux through the curved surface is

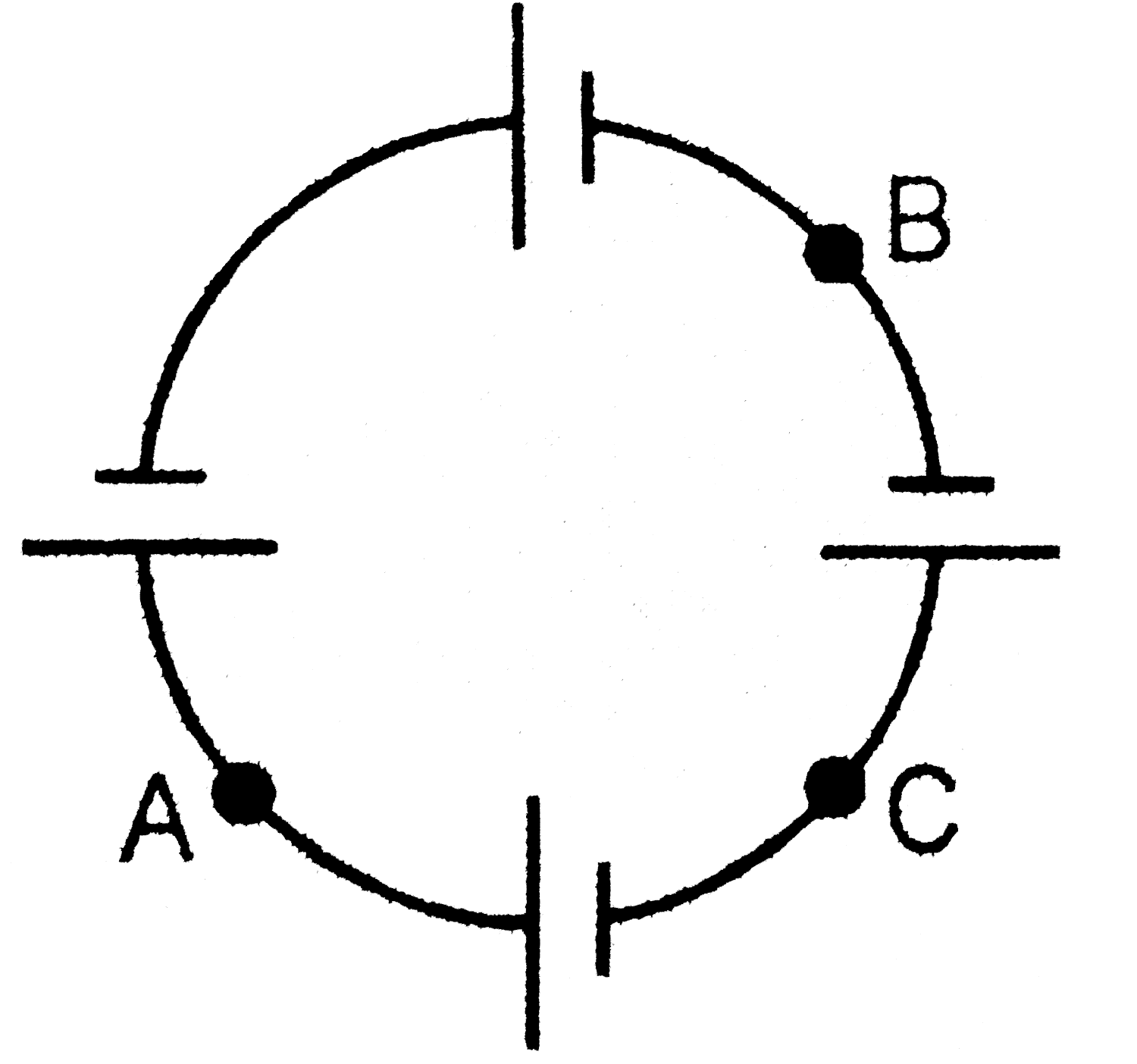
View SolutionFour idential cells each having e.m.f. E, internal resistance r are connected as shown in figure. Find the potential difference between: (i) A and B (ii) A and C
View Solution_2019_CBT3_E01_033_Q01.png)
A wire of length l and resistance R is bent in form of square as shown in figure. If E is a mid point of side D,A, then equivalent resistance between points E& A is:
View SolutionFind the equivalent resistance of the circuit shown in figure between the points a and b.Each resistor has a resistances r.

View SolutionFind out the flux through the curved surface of a hemisphere of radius R if it is placed in a uniform electric field E as shown in figure
View Solution

