A charged particle has acceleration →a=2ˆi+xˆj in a magnetic field →B=−3ˆi+2ˆj−4ˆk.Find the value of x.
∵→F⊥→B,∴→a⊥→B,∴→a.→B=0
∴(2ˆi+xˆj).(−3ˆi+2ˆj−4ˆk)=0⇒−6+2x=0→x=3
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-1
82 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-2
54 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
29 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
The magnetic moment of a short dipole is 1Am2.What is the magnitude of the magnetic induction in air at 10cm from centre of the dipole on a line making an angle of 30∘ from the axis of the dipole?
View SolutionTwo identical magnetic dipoles of magnetic moments 1.0 A−m2 each, are placed at a separation of 2 m with their axes perpendicular to each other. The resultant magnetic field at a point midway between the dipoles is
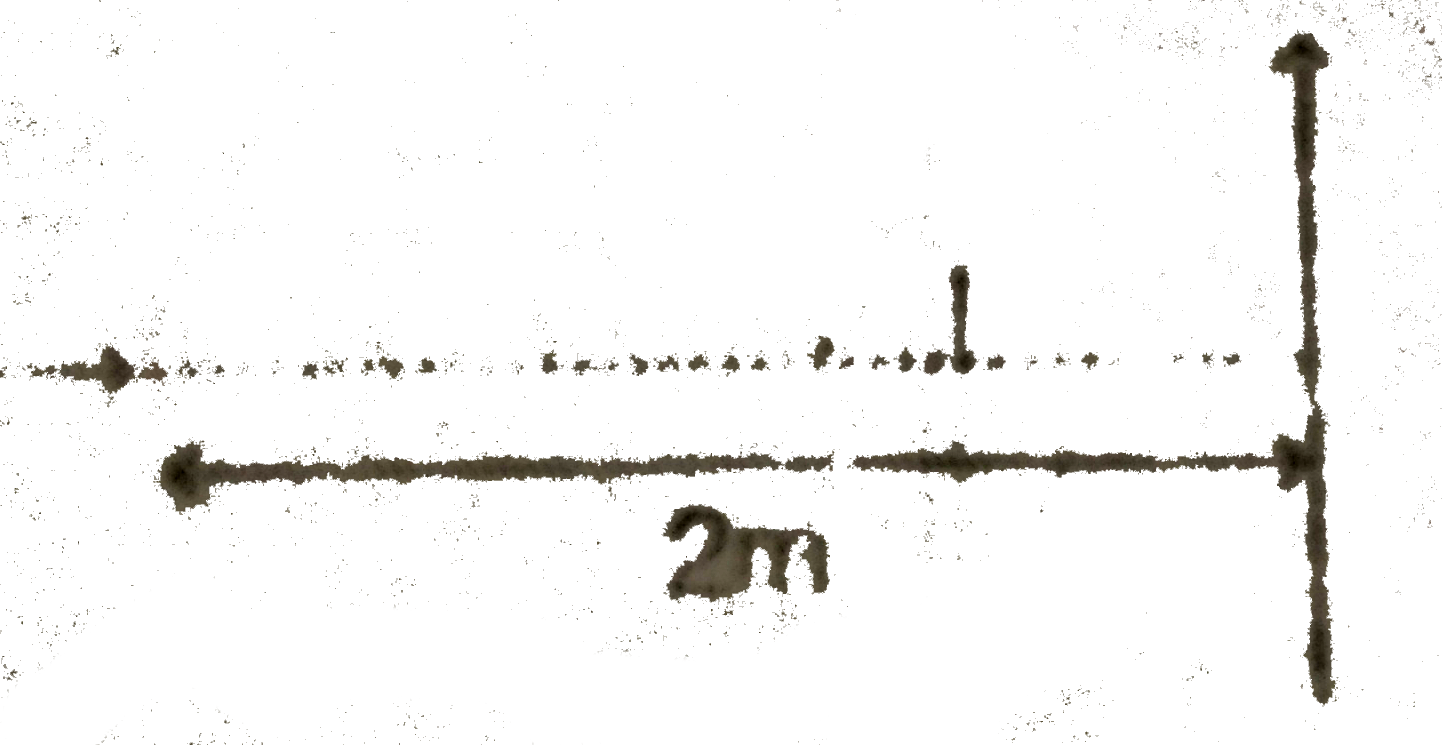
View SolutionCalculate the magnetic moment (in Am2 ) of a thin wire with a current I = 8A, wound tightly on half a torus (see figure). The diameter of the cross section of the torus is equal to d = 5 cm, and the number of turns is N = 500.

View SolutionAn electromagnetic wave of frequency υ=3 MHz passes from vacuum into a dielectric medium with permittivity ε=4. Then
View SolutionA long thin wire carrying a varying current I=i0sinωt lies at a distance y above one edge of a rectangular wire loop of length LandW lying in the x−z plane. What emf is induced in the loop?

View SolutionVelocity and acceleration vector of a charged particle moving in a magnetic field at some instant are vecv=3hati+4hatj and veca=2hati+xhatj . Select the correct options.
View SolutionIf →A=3ˆi+ˆj+2ˆk and →B=2ˆi−2ˆj+4ˆk, then value of ∣∣→A+→B∣∣ will be
View SolutionIf →A=3ˆi+ˆj+2ˆk and →B=2ˆi−2ˆj+4ˆk then value of ∣∣→A×→B∣∣ will be
View SolutionA charged particle has acceleration veca=2hati=xhatj in a magnetic field vecB=-3hati+2hatj-4hatk .Find the value of x .
View SolutionFind the angle 'θ' between the vector →a=2ˆi+3ˆj−4ˆk and →b=3ˆi−2ˆj+4ˆk.
View SolutionIf →a=2ˆi+3ˆj−4ˆk,→b=3ˆi−4ˆj−5ˆk, and→c=−3ˆi+2ˆj+3ˆk, find the magnitude and direction cosines of
→a+→b+→c
View Solution→a=3ˆi+ˆj+2ˆk এবং →b=2ˆi−2ˆj+4ˆk ভেক্টর দুটির মধ্যবর্তী কোণের কোসাইনের মান নির্ণয় করো ।
View SolutionIf →a=2ˆi+3ˆj−4ˆk,→b=3ˆi−4ˆj−5ˆk and →c=−3ˆi+2ˆj+3ˆk, find the magnitude and direction cosines of →a+→b+→c.
View SolutionFor what value of x, the vector →A=3ˆi+xˆj−4ˆk is perpendicular to be vector →B=2ˆi−2ˆj+6ˆk?
View SolutionA charged particle is inside a magnetic field vecB = (10hati - 6hatj) xx 10^(-4) T . The acceleration of the charged particle is given by veca = 3hati + xhatj m//s^(2) . What should be the value of x for this to be possible?
View SolutionA charged particle has acceleration →a=2ˆi=xˆj in a magnetic field →B=−3ˆi+2ˆj−4ˆk.Find the value of x.
View Solution

