If two charged particles of same mass and charge are describing circles in the same magnetic field with radii r1 and r2(>r1) the speed of the first particle is … that of the second particle while the time period of the particle is …that of the second partilcle.
The correct Answer is:A
To solve the problem, we need to analyze the motion of two charged particles moving in a magnetic field. Let's denote the two particles as Particle 1 and Particle 2, with radii r1 and r2 respectively, where r2>r1.
1. Understanding the Forces:
The magnetic force acting on a charged particle moving in a magnetic field provides the centripetal force necessary for circular motion. The magnetic force F on a charged particle is given by:
F=qvB
where q is the charge, v is the speed of the particle, and B is the magnetic field strength.
2. Centripetal Force:
The centripetal force required to keep a particle moving in a circle of radius r is given by:
F=mv2r
where m is the mass of the particle.
3. Equating Forces:
Since the magnetic force acts as the centripetal force, we can set these two equations equal to each other for both particles:
qv1B=mv21r1(for Particle 1)
qv2B=mv22r2(for Particle 2)
4. Solving for Speed:
From the above equations, we can express the speeds in terms of the radii:
v1=qBr1mandv2=qBr2m
Taking the ratio of the speeds:
v1v2=r1r2
5. Time Period Calculation:
The time period T for circular motion is given by:
T=2πrv
For both particles, we can write:
T1=2πr1v1andT2=2πr2v2
6. Taking the Ratio of Time Periods:
Now, substituting the expressions for v1 and v2:
T1=2πr1qBr1m=2πmqB
T2=2πr2qBr2m=2πmqB
Thus, the ratio of the time periods is:
T1T2=1
Final Answers:
- The speed of the first particle is proportional to that of the second particle, specifically v1v2=r1r2.
- The time period of the first particle is equal to that of the second particle, T1=T2.
The magnetic force acting on a charged particle moving in a magnetic field provides the centripetal force necessary for circular motion. The magnetic force F on a charged particle is given by:
F=qvB
where q is the charge, v is the speed of the particle, and B is the magnetic field strength.
The centripetal force required to keep a particle moving in a circle of radius r is given by:
F=mv2r
where m is the mass of the particle.
Since the magnetic force acts as the centripetal force, we can set these two equations equal to each other for both particles:
qv1B=mv21r1(for Particle 1)
qv2B=mv22r2(for Particle 2)
From the above equations, we can express the speeds in terms of the radii:
v1=qBr1mandv2=qBr2m
Taking the ratio of the speeds:
v1v2=r1r2
The time period T for circular motion is given by:
T=2πrv
For both particles, we can write:
T1=2πr1v1andT2=2πr2v2
Now, substituting the expressions for v1 and v2:
T1=2πr1qBr1m=2πmqB
T2=2πr2qBr2m=2πmqB
Thus, the ratio of the time periods is:
T1T2=1
- The speed of the first particle is proportional to that of the second particle, specifically v1v2=r1r2.
- The time period of the first particle is equal to that of the second particle, T1=T2.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-2
54 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - PROBLEM
12 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Two identical magnetic dipoles of magnetic moments 1.0 A−m2 each, are placed at a separation of 2 m with their axes perpendicular to each other. The resultant magnetic field at a point midway between the dipoles is
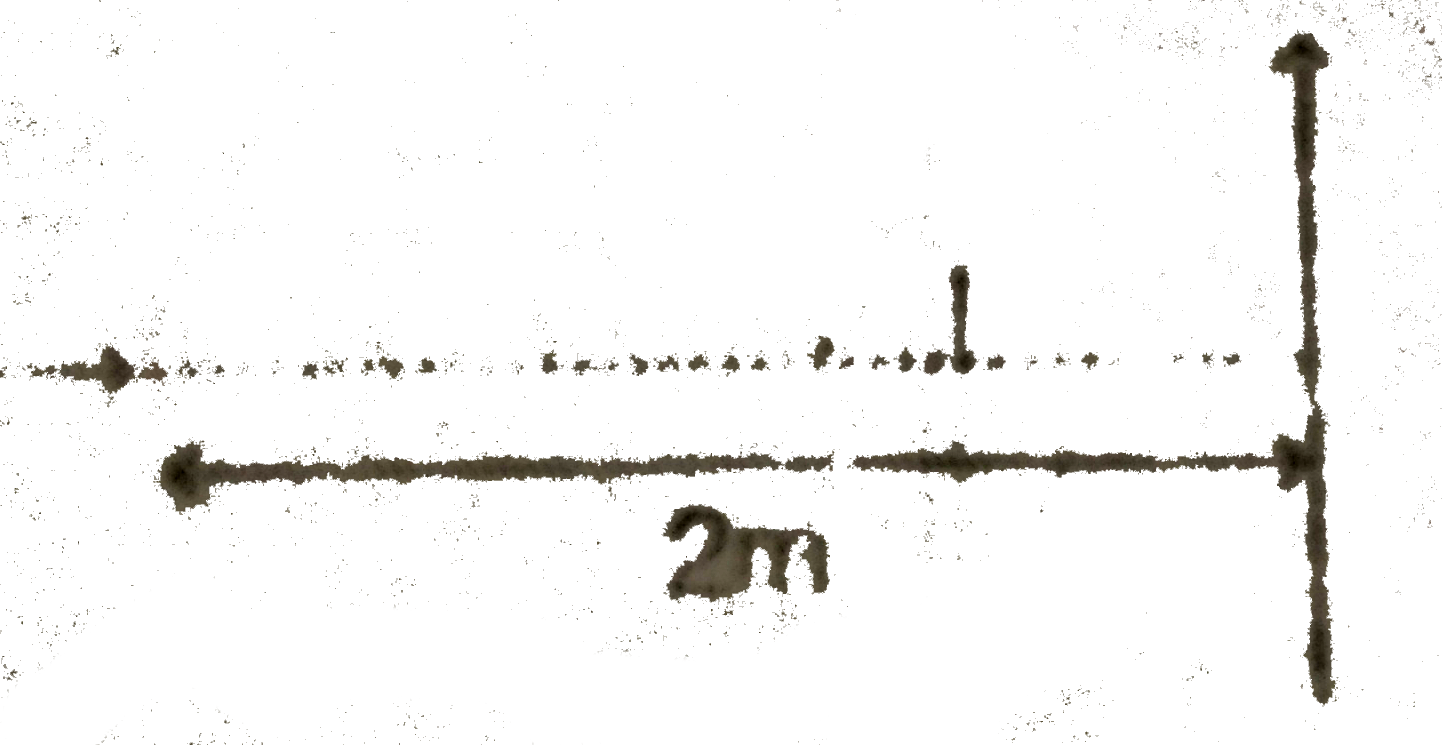
View SolutionAn α particle is moving along a circle of radius R with a constant angular velocity ω. Point A lies in the same plane at a distance 2R from the centre. Point A records magnetic field produced by the α particle. If the minimum time interval between two successive times at which A records zero magnetic field is t1, the angular speed ω in terms of t is
View SolutionTwo short magnet A and B of magnetic dipole mement M1 and M2 respectively are placed as shown.The axis of A and the equatorial line of B are the same.Find the magnetic force on one magnet due to other.
View SolutionAn electromagnetic wave of frequency υ=3 MHz passes from vacuum into a dielectric medium with permittivity ε=4. Then
View SolutionA long thin wire carrying a varying current I=i0sinωt lies at a distance y above one edge of a rectangular wire loop of length LandW lying in the x−z plane. What emf is induced in the loop?

View SolutionThe charge on a particle Y is double the charge on particle X. These two particles X and Y after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is
View SolutionTwo particles of equal masses are revolving in circular paths of radii r_(1) and r_(2) respectively with the same speed. The ratio of their centripetal force is
View SolutionIf two charged particles of same mass and charge are describing circles in the same magnetic field with radii r1 and r2(>r1) the speed of the first particle is … that of the second particle while the time period of the particle is …that of the second partilcle.
View Solutionदो कण क्ष तथा य जिन पर बराबर के आवेश है समान विभवान्तर से त्वरति होने पर एकसमान चुंबकीय क्षेत्र में प्रवेश करते है तथा R1) व R2 त्रिज्याओं के वृत्तियाँ पथों पर चलते है। X के द्रव्यांन का Y के साथ अनुपात है:
View Solutionसमान द्रव्यमान वाले दो कण क्रमशः r1 व r2 त्रिज्या के वृत्ताकार पथों पर समान चाल से चल रहे हैं । उन पर आरोपित अभिकेंद्र बल का अनुपात हैं -
View SolutionTwo particles of masses m_a and m_b and same charge are projected in a perpendicular magnetic field . They travel along circular paths of radius r_(a) and r_(b) such that r_(a) gt r_(b) . Then which is true ?
View SolutionTwo particles of masses m_(1) and m_(2) are moving in concentric circle of radii r_(1) and r_(2) such that their period are same. Then the ratio of their centripetal acceleration is
View Solutionकण Y पर आवेश , कण X पर आवेश का दोगुना है । ये दोनों कण X एवं Y एक ही विभवांतर से त्वरित होकर एकसमान चुम्बकीय क्षेत्र में प्रवेश करने पर त्रिज्या क्रमशः R1वR2 के वृत्ताकार पथ में चलते हैं । कण X के द्रव्यमान तथा कण Y के द्रव्यमान का अनुपात होगा :
View Solutionसमान द्रव्यमान तथा आवेश के दो आवेशित कण किसी चुम्बकीय क्षेत्र में वृत्ताकार पथ में घूर्णन करते हैं। यदि इनकी त्रिज्याएं r1 तथा r2(>r1) है तो प्रथम कण का वेग द्वितीय कण की तुलना में....है जबकि प्रथम कण का आवर्तकाल द्वितीय कण की तुलना में.... है।
View Solutionसमान विद्युत आवेश वाले दो कण, समान गतिज ऊर्जा से एकसमान चुम्बकीय क्षेत्र में प्रवेश करते हैं। यदि उनके वृत्तीय पथों की त्रिज्याएं क्रमशः r1 व r2 हैं तब उनके द्रव्यमानों का अनुपात लिखिए।
View Solution

