If VS(t)=220√2sin(2π50t), find (a)i(t) ,(b)V(R) and (c )V(C)(t)
To solve the problem step-by-step, we will find the current i(t), the voltage across the resistor VR(t), and the voltage across the capacitor VC(t) based on the given voltage source VS(t)=220√2sin(2π50t).
Step 1: Identify the given voltage source
The voltage source is given as:
VS(t)=220√2sin(2π50t)
From this, we can identify:
- The peak voltage V0=220√2
- The RMS voltage Vrms=220V
- The angular frequency ω=2π×50=100πrad/s
Step 2: Calculate the impedance Z
For an R-C circuit, the impedance Z is given by:
Z=√R2+X2C
where XC=1ωC.
Step 3: Find the current i(t)
The RMS current Irms can be calculated using:
Irms=VrmsZ
The peak current I0 is given by:
I0=Irms√2=VrmsZ√2
Thus, the current as a function of time is:
i(t)=I0sin(ωt+ϕ)
where ϕ is the phase difference between the voltage and the current.
Step 4: Calculate the phase angle ϕ
The phase angle ϕ can be calculated using:
tan(ϕ)=XCR=1ωRC
Thus, we can find ϕ as:
ϕ=tan−1(1ωRC)
Step 5: Find the voltage across the resistor VR(t)
The voltage across the resistor is given by:
VR(t)=i(t)⋅R
Substituting i(t):
VR(t)=I0Rsin(ωt+ϕ)
Step 6: Find the voltage across the capacitor VC(t)
The voltage across the capacitor lags the current by 90 degrees:
VC(t)=i(t)⋅XC
Substituting i(t):
VC(t)=I0XCsin(ωt+ϕ−90∘)
Final Answers
- i(t)=I0sin(100πt+ϕ)
- VR(t)=I0Rsin(100πt+ϕ)
- VC(t)=I0XCsin(100πt+ϕ−90∘)
The voltage source is given as:
VS(t)=220√2sin(2π50t)
From this, we can identify:
- The peak voltage V0=220√2
- The RMS voltage Vrms=220V
- The angular frequency ω=2π×50=100πrad/s
For an R-C circuit, the impedance Z is given by:
Z=√R2+X2C
where XC=1ωC.
The RMS current Irms can be calculated using:
Irms=VrmsZ
The peak current I0 is given by:
I0=Irms√2=VrmsZ√2
Thus, the current as a function of time is:
i(t)=I0sin(ωt+ϕ)
where ϕ is the phase difference between the voltage and the current.
The phase angle ϕ can be calculated using:
tan(ϕ)=XCR=1ωRC
Thus, we can find ϕ as:
ϕ=tan−1(1ωRC)
The voltage across the resistor is given by:
VR(t)=i(t)⋅R
Substituting i(t):
VR(t)=I0Rsin(ωt+ϕ)
The voltage across the capacitor lags the current by 90 degrees:
VC(t)=i(t)⋅XC
Substituting i(t):
VC(t)=I0XCsin(ωt+ϕ−90∘)
- i(t)=I0sin(100πt+ϕ)
- VR(t)=I0Rsin(100πt+ϕ)
- VC(t)=I0XCsin(100πt+ϕ−90∘)
Topper's Solved these Questions
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Problem
Explore 14 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -1 Part-1
Explore 64 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 16 Videos
Similar Questions
When a voltage Vs=200√2sin(100t)V is applied to an ac circuit the current in the circuit is found to be i=2sin[ωt+(π/4)]A. Find the average power consumed in the circuit.
View SolutionWhen a voltage Vs=200√2sin(100t)V is applied to an ac circuit the current in the circuit is found to be i=2sin[ωt+(π/4)]A. Find the average power consumed in the circuit.
View SolutionIn an RC series circuit(in fig), the rms voltage of source is 200V and its frequency is 50 Hz, if R=100ΩandC=100πμF, find
(a) inpedance of the circuit.
(b) power factor angle,
(c ) power factor,
(d) current,
(e) maximum current
(f) voltage across R,
(g) voltage across C,
(h) maximum voltage across R,
(i) maximum voltage across C,
(j) <P>,
(k) <PR>.
(l) <PC>
(m) i(t), VR(t),andVC(t).

View SolutionAn AC voltage of V=220√2sin(100πt+π2)V is applied across a DC votlmeter, its reading will be
View SolutionIn the figure show,
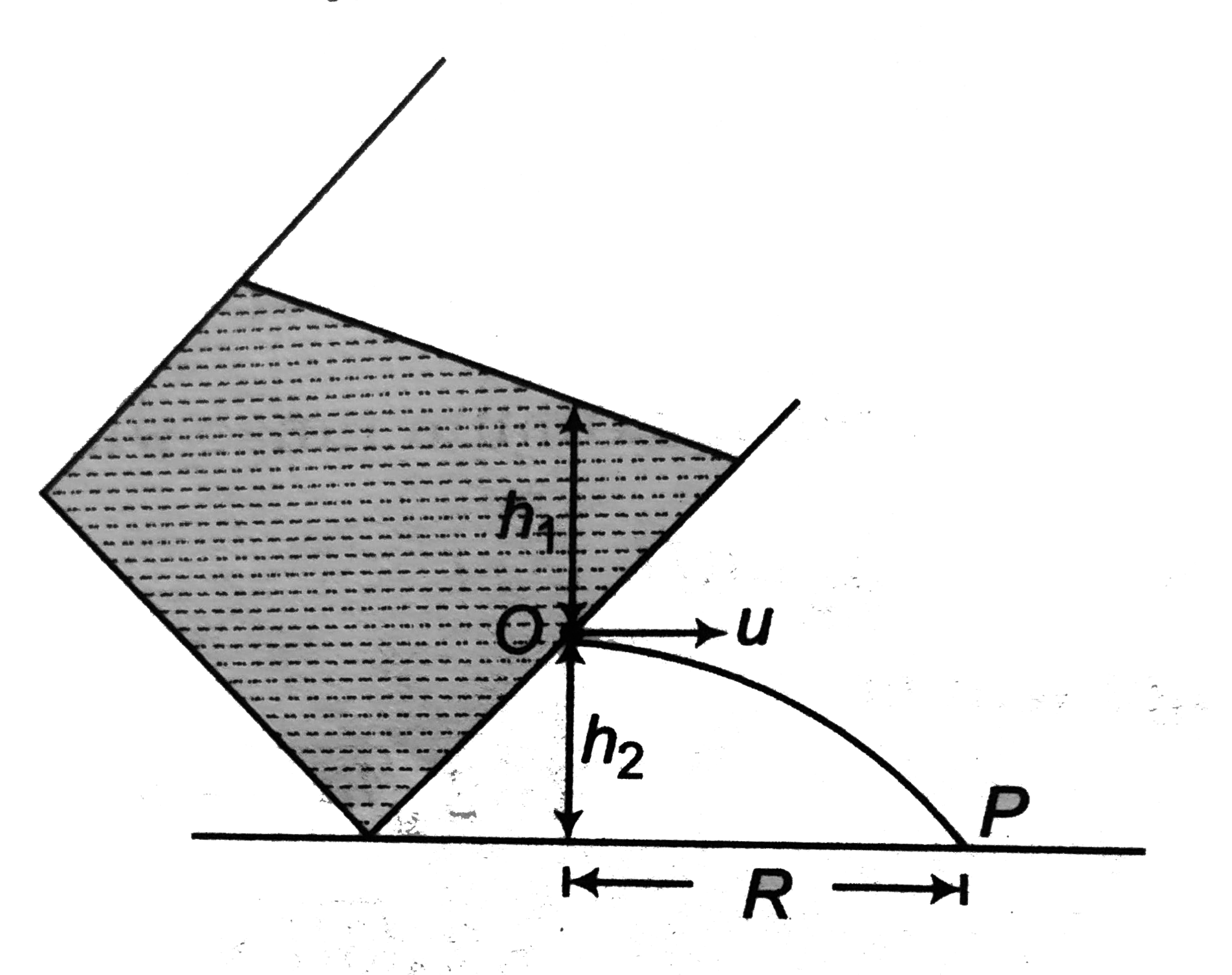
find v,top and R.
View SolutionIf the voltage in an ac circuit is represented by the equation,V=220√2sin(314t−ϕ) V. Calculate
(a) peak and rms.value of the voltage
(b) average voltage
(c) frequency of AC
View SolutionIn an L-C -R series circuit connected to an AC source V=V0sin(100π(t)+π6)VR=40V,VL=40andVC=10V, resistance R=4Ω
peak value of current is
View SolutionFollowing are equations of four waves :
(i) y1=asinω(t−xv)
(ii) y2=acosω(t+xv)
(iii) z1=asinω(t−xv)
(iv) z1=acosω(t+xv)
Which of the following statements are correct ?
View SolutionFollowing are equations of four waves :
(i) y1=asinω(t−xv)
(ii) y2=acosω(t+xv)
(iii) z1=asinω(t−xv)
(iv) z1=acosω(t+xv)
Which of the following statements are correct ?
View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View Solution
