An initially parallel cylindrical beam travels in a medium of refractive index μ(l)=μ0+μ2l, where μ0 and μ2 are positive constants and l is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
The speed of light in the medium is
minimum the axis of the beam
the same everywhere in the beam
directly proportional to the intensity I
maximum on the axis of the beam
The correct Answer is:A
μ=μ0+μ2(I)
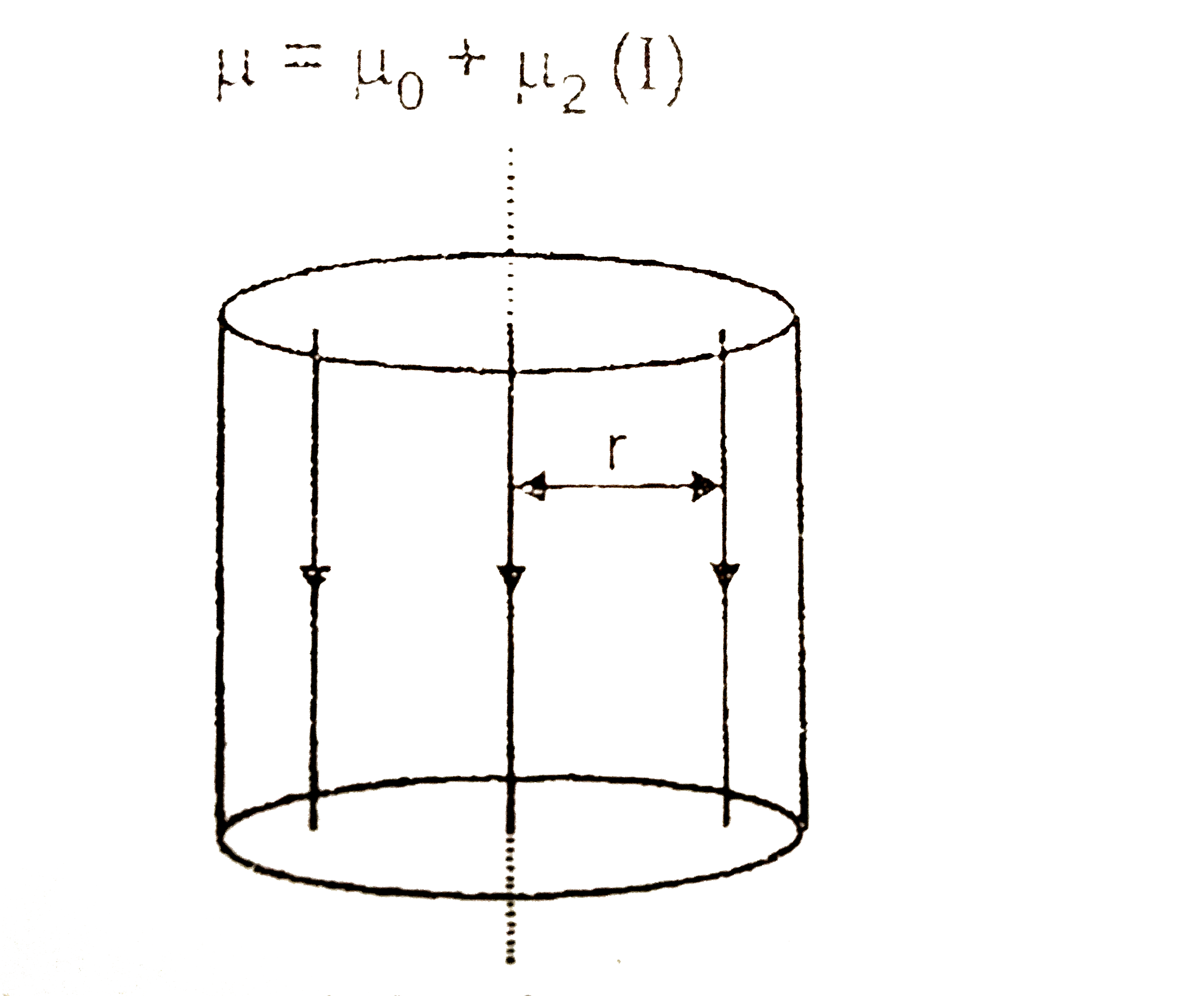
as it is given that intensity of beam is decreasing with increasing radius, and as I decreases μ also decreases.
Now by V=Cμ. Speed of light is minimum at axis of cylinder.
Topper's Solved these Questions
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Exercise-3 (Part-3)
Explore 22 Videos
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Advanced Level Problems
Explore 7 Videos
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Exercise-3 (Part-1)
Explore 11 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 3 PART II
Explore 7 Videos
Similar Questions
In a cyclotron, a charged particle
View SolutionTwo parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I and I, respectively, find the resultant intensity at the focus.
View SolutionA beam of monoenergetic electrons, which have been accelerated from rest by a potential U, is used to form an interference pattern in a Young's Double slit experiment. The electrons are now accelerated by potential 4U. The fringe width -
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionAn initially parallel cylindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
30 . At the beam enters the medium, it will
View SolutionAn initially parallel cylindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
32. The speed of light in the medium is
View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index mu (I) = mu_(0) + mu_(2) I , where mu_(0) and mu_(2) are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius. Answer the following questions : As the beam enters the medium, it will
View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
The speed of light in the medium is
View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
The initial shape of the wavefront of the beam is
View SolutionA concave lens having a material of refractive index μ1 is kept in a medium of R.I. μ2, where μ1<μ2. A parallel beam of light is incident on the lens. The concave lens will act as
View SolutionA convex lens of refractive index μ1 is kept in a medium of refractive index (μ2) . A parallel beam of light is incident on the lens . Draw the path of the rays of light emerging from a lens . If μ1=μ2
View SolutionA concave lens of refractive index mu_(1) is kept in a medium of refractive index (mu_(2)) . A parallel beam of light is incident on the lens . Draw the path of the rays of light emerging from a lens . If mu_(1) = mu_(2)
View Solutionप्रारम्भ में एक समान्तर बेलनाकार पुंज किसी माध्यम जिसका अपवर्तनांक μ=μ0+μ2I है, में प्रवेश करता है, जहाँ μ0 तथा μ2 धनात्मक नियतांक है तथा I प्रकाश पुंज की तीव्रता है | त्रिज्या बढ़ाने पर पुंज की तीव्रता घटती है | (i) जैसे ही पुंज माध्यम में प्रवेश करता है, यह :
View SolutionAn initially parallel cylindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0andμ2 are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
The initial shape of the wavefront of the beam is :
View SolutionAn initially parallel cylindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0andμ2 are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
The speed of light in the medium is :
View SolutionAn initially parallel cylindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0andμ2 are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
As the beam enters the medium, it will :
View Solution
