The transverse displacement of a string (clamped at its ends) is given by y(x,t)=0.06sin(2π/33)×cos120πt where x,y are in m and t is in s. the length of the string is 1.5 m and its mass is 3.0×10−2 kg. answer the following.
(i) Does the function represent a travelling or a stationary wave?
(ii) Interpret the wave as a superposition of two waves travelling in opposite directions. What are the wavelength frequency and speed of propagation of each wave ?
(iii) Determine the tension in the string.
The correct Answer is:(a) Stationary wave
(b) l=3m,n=60Hz, and u=180ms−1 for each wave
(c) 648N
Step by step video solution for The transverse displacement of a string (clamped at its ends) is given by y(x,t)=0.06sin((2pi//3)/(3))xxcos120pit where x,y are in m and t is in s. the length of the string is 1.5 m and its mass is 3.0xx10^(-2) kg. answer the following. (i) Does the function represent a travelling or a stationary wave? (ii) Interpret the wave as a superposition of two waves travelling in opposite directions. What are the wavelength frequency and speed of propagation of each wave ? (iii) Determine the tension in the string. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 1 PART I
23 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 1 PART II
30 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Solved Miscellaneous Problems
7 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART II
7 Videos
Similar Questions
Consider the wave y=(5mm)sin[1cm−1x−(60s−1)t]. Find (a) the amplitude, (b) the angular wave number, ( c ) the wavelength, (d) the frequency, (e) the time period and (f) the wave velocity.
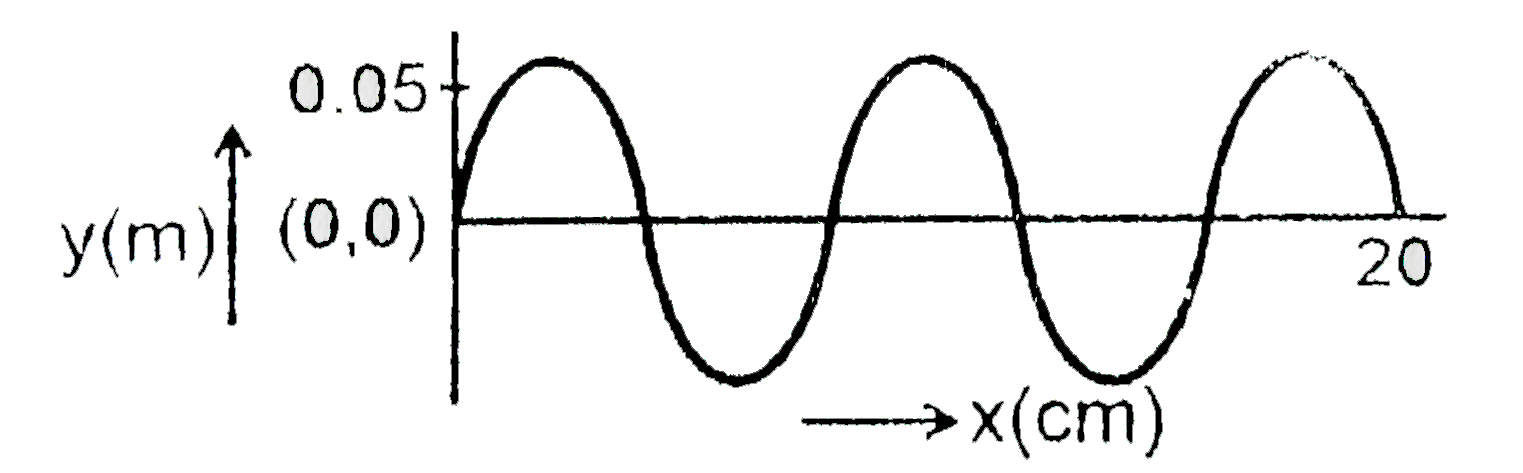
View SolutionFor the wave shown in figure, the equation for the wave, travelling along +x acis with velocity 350ms−1 when its position at t=0 is as shown
View SolutionA wave pulse moving along the x axis is represented by the wave function
y(x,t)=2(x−3t)2+1
where x and y are measured in cm and t is in seconds.
(i) in which direction is the wave moving ?
(ii) Find speed of the wave.
View SolutionA time varying voltage is applied across A & B such that voltage across capacitor is given by VC=2sin2t. What is maximum potential difference across the reistance?

View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionThe transverse displacement of a string (clamped at its two ends ) is given by
y(x,t)=0.06sin(2π3)xcos(120πt)
wherer x ,y are in m and t ini s. The length of the string is 1.5m and its mass is 3×10−2 kg. Answer the following: (i) Does the function represent a travelling or a stationary wave ?
(ii) Interpret the wave as a superimposition of two waves travelling in opposite directions. What are the wavelength, frequency and speed of propagation of each wave ?
(iii) Determing the tension in the string.
View SolutionThe transvers displacement of a string (clamped at its both ends) is given by
y(x,t)=0.06sin(2π3s)cos(120πt)
Where x and y are in m and t in s. The length of the string 1.5m and its mass is 3.0×10−2kg.
Answer the following :
(a) Does the funcation represent a travelling wave or a stational wave ?
(b) Interpret the wave as a superposition of two waves travelling in opposite directions. What is the wavelength. Frequency and speed of each wave ?
Datermine the tension in the string.
View SolutionThe transverse displacement of a string clamped at its both ends is given by y(x, t) = 0.06 sin ((2pi)/3 x) cos(l20pit) where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3 xx 10^(-2) kg. The tension in the string is
View SolutionThe transverse displacement of a string ( clamped at its both ends ) is givenby y(x,t)=0.06sin(2π3x)cos(120πt)
where x and y are in m and t in s. The length of the string is 1.5m and its mass is 3.0×10−2kg
Answer the following :
(a) Does the function represent a travelling wave or a stationary wave ?
(b) Interpret the wave as a superposition of two waves travelling in opposite directios. What is the wavelength, frequency,and speed of each wave ?
(c ) Determine the tension in the string.
View SolutionThe transverse displacement of a string is given by y(x,t)=0.06sin(2π3)xcos(120πt) where 'x' & 'y' are 'm' and 't' is s. The length of the string is 1.5m and its mass is 3.0×10−2kg.
Does the function represent a travelling wave or stationary wave ?
View SolutionThe transverse displacement of a string (clamped at its two ends ) is given by
y(x,t)=0.06sin(2π3)xcos(120πt)
wherer x ,y are in m and t ini s. The length of the string is 1.5m and its mass is 3×10−2 kg. Answer the following: (i) Does the function represent a travelling or a stationary wave ?
(ii) Interpret the wave as a superimposition of two waves travelling in opposite directions. What are the wavelength, frequency and speed of propagation of each wave ?
(iii) Determing the tension in the string.
View SolutionThe transverse displacement of a string (clamped at its both ends) is given by y (x , t) = 0 . 0 6 sin ((2pi)/(3) x) cos (120 pi t) Where x and y are in m and t in s . The length of the string is 1 . 5 m and its mass is 3 . 0 xx 10^(-2) kg . Answer the following , Does the funcation represent a travelling wave or a stationary wave ?
View SolutionThe transverse displacement of a string (clamped at its both ends) is given by y (x , t) = 0 . 0 6 sin ((2pi)/(3) x) cos (120 pi t) Where x and y are in m and t in s . The length of the string is 1 . 5 m and its mass is 3 . 0 xx 10^(-2) kg . Answer the following , Interpret the wave as a superposition of two waves travelling in opposite directions . What is the wavelength, frequency and speed of each wave ?
View SolutionThe transverse displacement of a string (clamped at its both ends) is given by
y(x,t)=0.06sin(2x3x)cos(120πt)
where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0×10−2kg.
Answer the following :
(a) Does the function represent a travelling wave or a stationary wave?
(b) Interpret the wave as a superposition of two waves travelling in opposite directions. What is the wavelength, frequency , and speed of each wave ?
(c ) Determine the tension in the string.
View SolutionThe transverse displacement of a string (clamped at its both ends) is given by y(x, t) = 0.06 sin ((2 x)/(3) x) cos (120 pi t) where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0 xx 10^(-2) kg . Answer the following : (a) Does the function represent a travelling wave or a stationary wave? (b) Interpret the wave as a superposition of two waves travelling in opposite directions. What is the wavelength, frequency , and speed of each wave ? (c ) Determine the tension in the string.
View SolutionThe transvers displacement of a string (clamped at its both ends) is given by y(x,t) = 0.06 sin ((2pi)/(3)s) cos (120 pit) Where x and y are in m and t in s . The length of the string 1.5 m and its mass is 3.0 xx 10^(-2) kg . Answer the following : (a) Does the funcation represent a travelling wave or a stational wave ? (b) Interpret the wave as a superposition of two waves travelling in opposite directions. What is the wavelength. Frequency and speed of each wave ? Datermine the tension in the string.
View Solution

