The equation of a plane wave travelling along positive direction of x−axis is y=asin2πλ(vt−x) When the wave is reflected at a rigid surface and its amplitude becomes 80%, then find the equation of the reflected wave.
The correct Answer is:y'=0.8asin(2π)λ(vt+x+λ2).
To find the equation of the reflected wave when a plane wave traveling along the positive x-axis reflects off a rigid surface and its amplitude becomes 80%, we can follow these steps:
Step 1: Write the equation of the original wave
The equation of the wave traveling along the positive x-axis is given as:
y=asin(2πλ(vt−x))
Step 2: Determine the amplitude of the reflected wave
When the wave is reflected at a rigid surface, the amplitude of the reflected wave becomes 80% of the original amplitude. Therefore, the amplitude of the reflected wave is:
Areflected=0.8a
Step 3: Determine the direction of the reflected wave
The reflected wave travels in the opposite direction to the original wave. Therefore, we need to change the sign of the x term in the wave equation.
Step 4: Write the equation of the reflected wave
The general form of the wave traveling in the negative x-direction can be written as:
y=Asin(2πλ(vt+x+ϕ))
where ϕ is the phase difference due to reflection. Since the wave reflects off a rigid boundary, the phase difference is λ2.
Thus, substituting the amplitude and the phase difference, the equation of the reflected wave becomes:
y=0.8asin(2πλ(vt+x+λ2))
Final Equation
Therefore, the final equation of the reflected wave is:
y=0.8asin(2πλ(vt+x+λ2))
---
The equation of the wave traveling along the positive x-axis is given as:
y=asin(2πλ(vt−x))
When the wave is reflected at a rigid surface, the amplitude of the reflected wave becomes 80% of the original amplitude. Therefore, the amplitude of the reflected wave is:
Areflected=0.8a
The reflected wave travels in the opposite direction to the original wave. Therefore, we need to change the sign of the x term in the wave equation.
The general form of the wave traveling in the negative x-direction can be written as:
y=Asin(2πλ(vt+x+ϕ))
where ϕ is the phase difference due to reflection. Since the wave reflects off a rigid boundary, the phase difference is λ2.
y=0.8asin(2πλ(vt+x+λ2))
Therefore, the final equation of the reflected wave is:
y=0.8asin(2πλ(vt+x+λ2))
Topper's Solved these Questions
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 1 PART II
Explore 30 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 2 PART I
Explore 21 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Board Level Exercise
Explore 27 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 3 PART II
Explore 7 Videos
Similar Questions
For the wave shown in figure, the equation for the wave, travelling along +x acis with velocity 350ms−1 when its position at t=0 is as shown
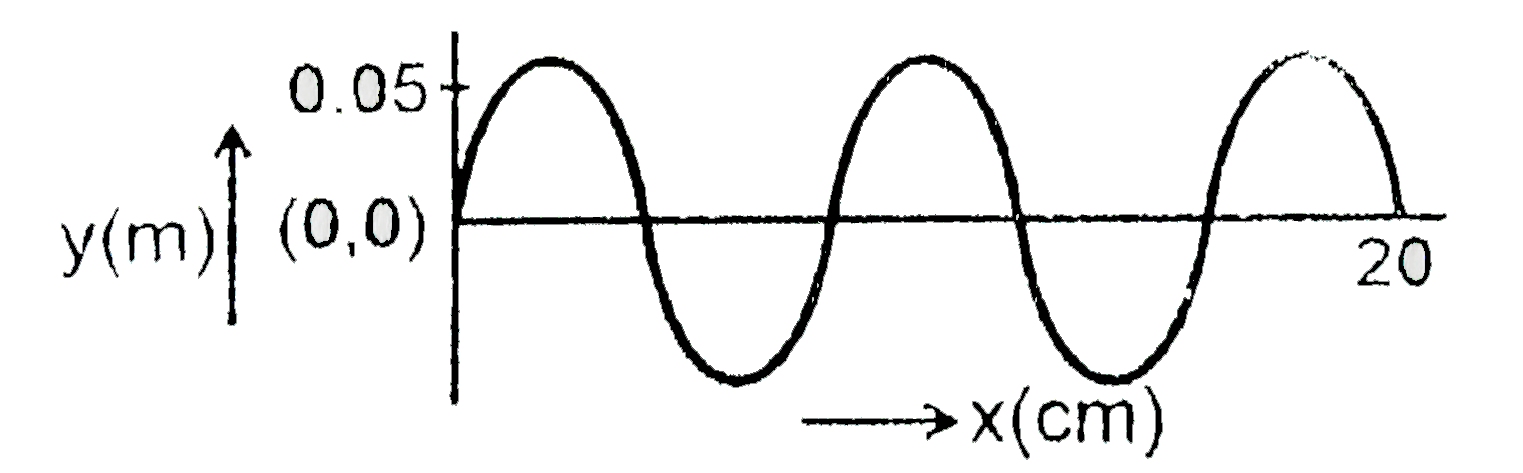
View Solutionthe same progressive wave is reprsented by two group I and II. Graoup I shows how the displacement 'y' varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curvse m repersents.
View SolutionWhat is a harmonic wave funcation ?
View SolutionA time varying voltage is applied across A & B such that voltage across capacitor is given by VC=2sin2t. What is maximum potential difference across the reistance?

View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionEquation of a plane progressive wave is given by y=0.6sin2π(t−x2). On reflection from a denser medium, its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is
View SolutionThe equation of a plane progressive wave is y = 0.9 "sin"4 pi [t - ("x")/(2)] . When it is reflected at a rigid support , its amplitude becomes (2)/(3) of its previous value. The equation of the reflected wave is
View SolutionA wave travelling along positive x -axis is given by y = A sin (omega t- kx) . If it is reflected from rigid boundary such that 80% amplitude is reflected, then equation of reflected wave is
View SolutionThe equation of a plane wave travelling along positive direction of x−axis is y=asin2πλ(vt−x) When the wave is reflected at a rigid surface and its amplitude becomes 80%, then find the equation of the reflected wave.
View SolutionX- अक्ष दिशा में जाने वाली एक प्रगामी तरंग का समीकरण y=0.06sin2π(200t−x) है। यह तरंग एक दृढ़ तल से परावर्तित होती है, तो उसका आयाम पहले का 1/3 रह जाता है। पावर्तित रंग का समीकरण ज्ञात कीजिए।
View SolutionX अक्ष की धन दिशा में जाने वाली एक प्रगामी तरंग का समीकरण y=0.06sin2π(200t−x) है|यह तरंग एक दृढ़ तल से परावर्तित होती है तथा इसका आयाम पहले से 13 भाग आधा रह जाता है|
(i) परावर्तित तरंग की समीकरण ज्ञात कीजिए|(ii ) यदि यह तरंग किसी मुक्त तल से परावर्तित हो तो परावर्तित तरंग की समीकरण क्या होगी?
View SolutionThe equation of a wave is y=A sin (2pint) When it is reflected at a free end its amplitude becomes 90% The equation of the reflected wave is
View SolutionAn incident wave and a reflected wave are represented by
ξ1=asin2πλ(vt−x)andξ2=asin2πλ(vt+x)
Derive the equation of the stationary wave and calcu-late the position of the nodes and antinodes.
View SolutionThe equation of a waves is y = sin (2pi rt//lambda) . When it is reflected to at a rigid support its amplitude reduces by 10%. The equation of the replaced wave
View SolutionEquation of a plane progressive wave u=0.6 sin 2pi (t-x/2) Is, when reflected through a dense medium, its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is
View Solution
