Two coils connected in series have resistance of 600KΩ and 300Ω at 20∘C and temperature coefficient of0.001 and 0.004(.∘C)−1 respectively. Find resistance of the combination at a temperature of 50∘C. What is the effective temperature coefficient of combination?
11000degree−1
1250degree−1
1500degree−1
31000degree−1
The correct Answer is:B, C
Step by step video solution for Two coils connected in series have resistance of 600K Omega and 300 Omega at 20^@C and temperature coefficient of 0.001 and 0.004 (.^@C)^-1 respectively. Find resistance of the combination at a temperature of 50^@C. What is the effective temperature coefficient of combination? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise-1 (Part-3)
Explore 2 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise-2 (Part-1)
Explore 24 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise-1 (Part-1)
Explore 41 Videos
- COMMUNICATION SYSTEMSBook:RESONANCE ENGLISHChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP.No.71
Explore 1 Video
Similar Questions
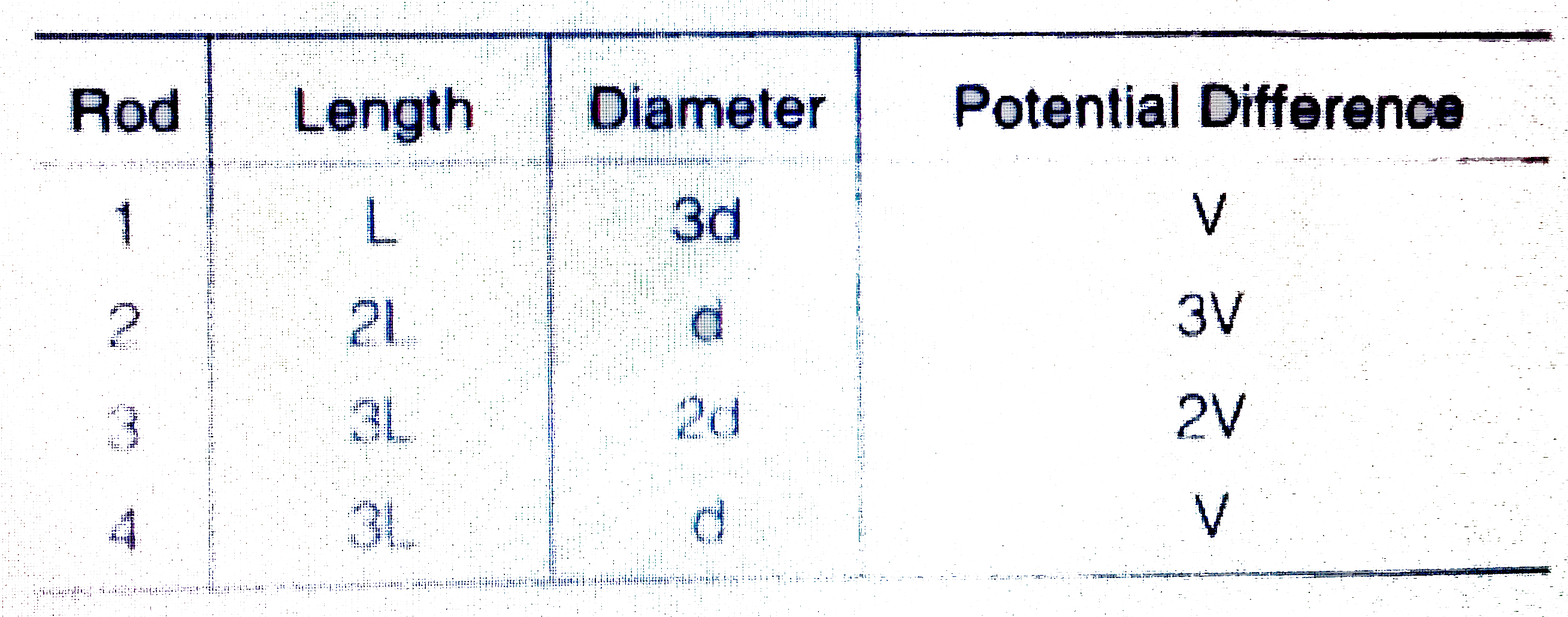
the following table gives the lengths of four copper rods at the temperature ,their diameters and the potential differences between their ends.

View SolutionIf a copper wire is stretched to make it 0.1% longer, then the percentage change in resistance is approximately -
View SolutionThe current through a wire depends on time as
I=i0+αt,
where i0=10Aandα=4As−1.Find the charge crossed through a section of the wire in 10 second
View SolutionConsider telecommunication through optical fibers. Which of the following statements is not true ?
View SolutionConsider a uniform wire of length l. Cross-sectional area A, Young's modulus of the material of the wave is Y. Some information related to the wire is given in column-1 and dependence of the result is given in column-2. Then match the approprite choice between the columns and match the list given in options
Column-I Column-II(A) Let us suspend wire vertically from a (p) Young'sModulusrigud support and attach a mass m atits lower end. If the mass is slightly pulleddown and released, it executes S.H.Mof a time period which will depend on(B) Work done in stretching the wire up to length (q) elongation (x)l+xwill depend on(C) If the given is fixed between two rigid (r) length (l)supports and its temperature is decreasedthermal stress that develops in the wirewill depend on(D) If the wire is pulled at its ends equal and (s) area of cross-section (A) opposite forces of magnitude F so that itundergoes an elongation x, according toHook's law, F=kx, where k is the forceconstant.Force constant (k) of the wirewill depend on
View SolutionTwo coils connected in series have resistance of 600K Omega and 300 Omega at 20^@C and temperature coefficient of 0.001 and 0.004 (.^@C)^-1 respectively. Find resistance of the combination at a temperature of 50^@C . What is the effective temperature coefficient of combination?
View SolutionA copper coil has resistance of 20.0Ωat0∘C and a resistance of 26.4Ωat80∘C. Find the temperature coefficient of resistance of copper.
View SolutionA tungsten coil has a resistance 16 Omega at 20^@C . If the temperature coefficient of resistance of tungsten is 0.004^@C^(-1) , calculate the resistance of the coil at 80^@C .
View SolutionTwo wires of different materials P and Q have resistance per unit lengths 50Ωkm−1 and 25Ωkm−1 and temperature coefficients of resistance, 0.0025∘C−1 and 0.00075∘C−1 respectively. If it is desired to make a coil having 700Ω resistance and a temperature coefficient of resistance 0.001∘C−1 by using suitable length of two wires in series. Calculate their respective length.
View SolutionThe temperature coefficient of resistance of the material of a wire is 0.00125∘C−1. Its resistance at 27∘C is 1Ω. At what temperature will its resistance be 2Ω ?
View SolutionA carbon filament has a resistance of 100Ω at 0∘C. What must be the resistance of a copper filament placed in series with carbon so that the combination has the same resistance at all temperatures ? Temperature coefficient of resistance of carbon =−0.0007.∘C−1 and that of copper is 0.004∘C−1.
View SolutionA standard coil marked 3 Omega is found to have a true resistance of 3.115 Omega at 300 K. Calculate the temperature at which marking is correct. Temperature coefficient of resistance of the material of the coil is 4.2xx10^(-3) .^(@)C^(-1) .
View SolutionThe temperature coefficient of a resistance wire is 0.00 12^(@)C^(-1) . At 300 K, its resistance is 1 Omega . At what temperature the resistance of the wire will be 2 Omega ?
View SolutionThe temperature coefficient of resistance of a metal is 0.004 ^@C^-1 . If a wire has resistance 1 Omega at 0^@C then what will be the value of that resistance at 100^@C ?
View SolutionThe resistance of a copper wire is 20 Omega at 0^@C . Find the resistance at 60^@C if the temperature coefficient of resistance of material is 0.004//^@C .
View SolutionTwo coils connected in series have resistance of 600K Omega and 300 Omega at 20^@C and temperature coefficient of 0.001 and 0.004 (.^@C)^-1 respectively. Find resistance of the combination at a temperature of 50^@C . What is the effective temperature coefficient of combination?
View Solution
