A particle is taken to a distance r (gt R) from centre of the earth. R is radius of the earth. It is given velocity V which is perpendicular to With the given values of V in column I you have to match the values of total energy of particle in column II and the resultant path of particle in column III. Here 'G' is the universal gravitational constant and 'M' is the mass of the earth.

The correct Answer is:A, B, C, D
Step by step video solution for A particle is taken to a distance r (gt R) from centre of the earth. R is radius of the earth. It is given velocity V which is perpendicular to With the given values of V in column I you have to match the values of total energy of particle in column II and the resultant path of particle in column III. Here 'G' is the universal gravitational constant and 'M' is the mass of the earth. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2 PART-1
15 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2 PART-2
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXERCISE-1 PART-2
21 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
33 Videos
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions
16 Videos
Similar Questions
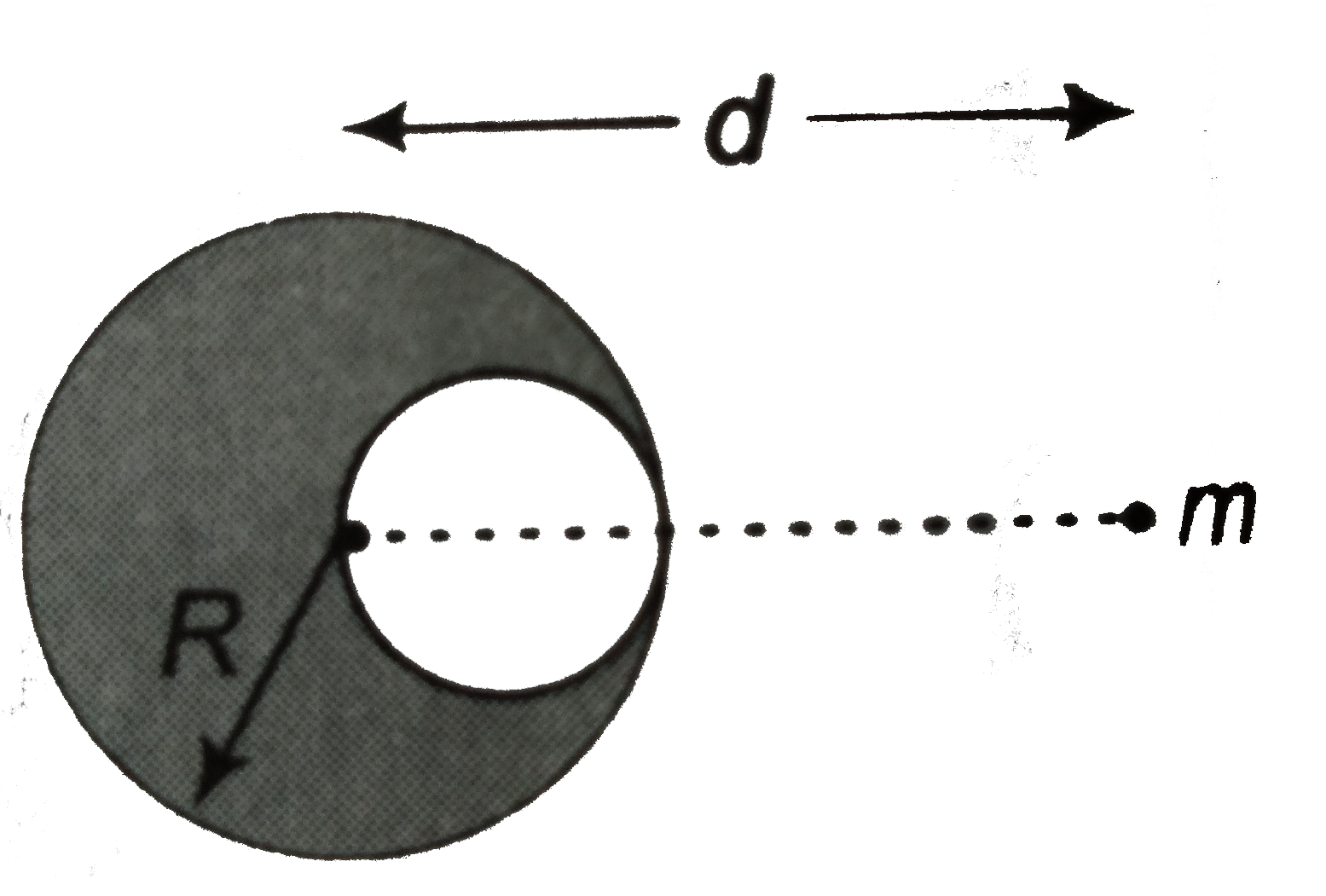
Figure shows a spherical cavity inside a lead sphere. The surface of the cavity passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was M. With what gravitational force does the hollowed out lead sphere attract a particle of mass m that lies at a distance d from the centre of the lead sphere on the straight line connecting the centres of the spheres and of the cavity.
View SolutionThere is crater of depth R/100 on the surface of the moon (raduis R). A projectile is fired vertically upwards from the crater with a velocity, which is equal to the escape velocity v from the surface of the moon. The maximum height attained by the projectile, is :
View SolutionFour similar particles of mass m are orbiting in a circle of radius r in the same direction and same speed because of their mutual gravitational attractive force as shown in the figure . Speed of a particle is given by
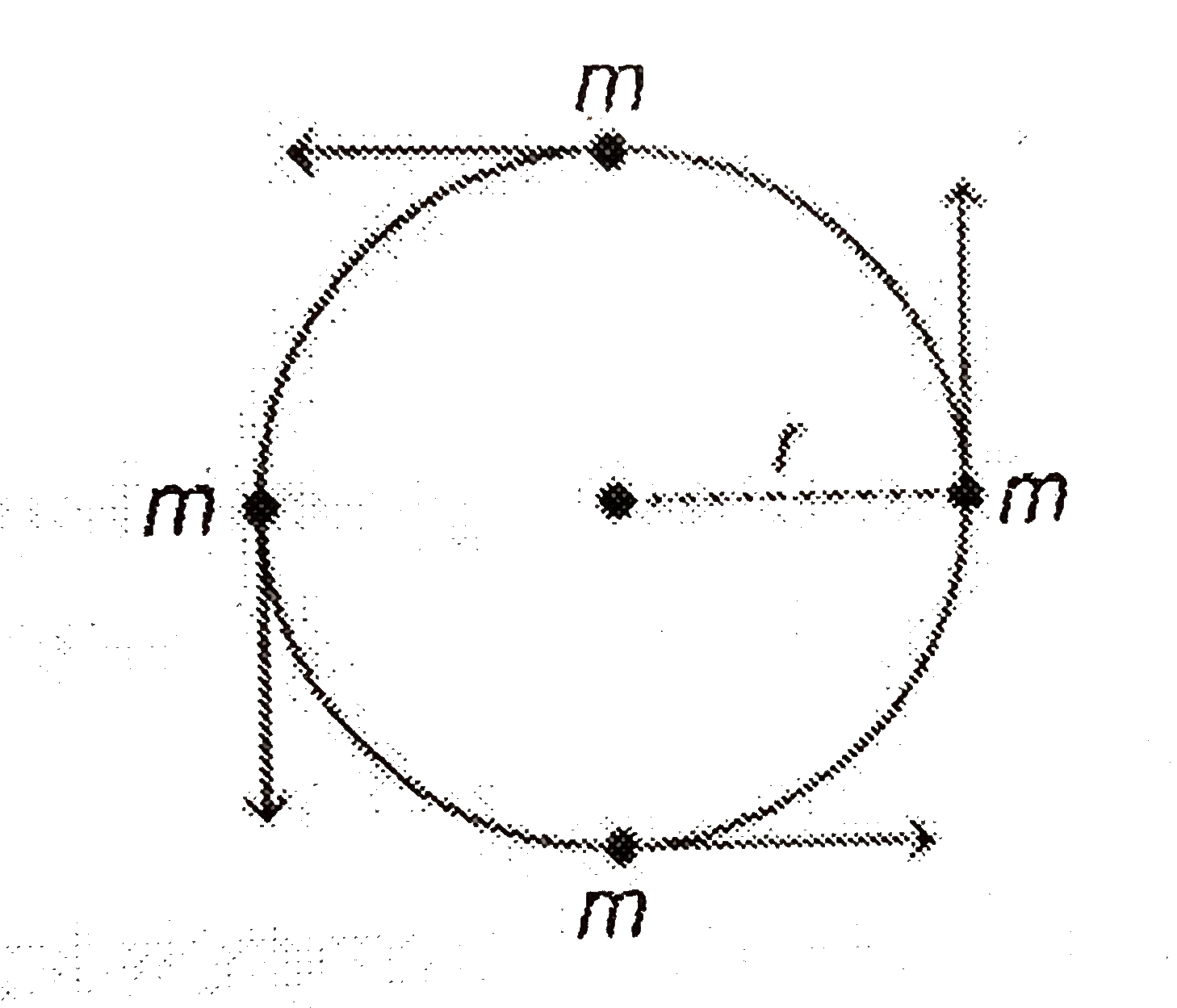
View SolutionA U-shaped wire is placed before a concave having radius of curvature 20 cm as shown (18-E1). Find the total length of the image.

View SolutionA radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View SolutionMatch the column : A particle at a distance r from the centre of a uniform spherical planet of mass M radius R(lt r) has a velocity v magnitude of which is given in column I. Match trajectory from column II about possible nature of orbit. {:(,"Column I",,"Column II"),((A),0lt V lt sqrt((GM)/(r )),(P),"Straight line"),((B),sqrt((GM)/(r )),(Q),"Circle"),((C ),sqrt((2GM)/(r )),(R ),"Parabola"),((D),v gt sqrt((2GM)/(r )),(S ),"Ellipse"):}
View SolutionOn the surface of earth acceleration due gravity is g and gravitational potential is V. Match of following columns
Column-IColumn-II(A)At height h=R, value of g(p)Decreases by a factor14(B)At depth h=R2,value of g(q)Decrease by a factor12(C)At height h=R,value of V(r)Increase by a factor118(D)At height h=R2,value of V(s)Increase by a factor 2(t)None
View SolutionMatch the column-I to value of Tension given in column-II, assuming mass of particle equal to m

View SolutionA particle is taken to a distance r (gt R) from centre of the earth. R is radius of the earth. It is given velocity V which is perpendicular to With the given values of V in column I you have to match the values of total energy of particle in column II and the resultant path of particle in column III. Here 'G' is the universal gravitational constant and 'M' is the mass of the earth.
View SolutionMatch the items in column I to the items in column II given below : G = universal gravitational constant, M = mass of earth, R = radius of earth
Column -IColumn -II(A)Escape velocity from a height R above earth's surface(p)√4GMR(B)Minimum horizontal velocity required for a particle at a height R above earth's surface to avoid falling on earth(q)√GMR(C)Escape valocity on the surface of earth if earth's diameter were shrunk to half of its present value(r)√GM3R(D)Velocity of a body thrown from the earth's surface to reach a height of R3 from the surface of the earth(s)√GM2R
View SolutionA particle is projected vertically with speed V from the surface of the earth . Maximum height attained by the particle , in term of the radius of earth R,V and g is ( V < escape velocity , g is the acceleration due to gravity on the surface of the earth )
View Solutionm द्रव्यमान का एक कण पृथ्वी तल से ऊपर की ओर u वेग से फेंका जाता है | पृथ्वी का द्रव्यमान तथा त्रिज्या क्रमशः M ओर R है | पृथ्वी तल पर गुरुत्वाकर्षण नियतांक G तथा गुरुत्वीय त्वरण g है | u का वह न्यूनतम मान, जिससे कण पृथ्वी तल पर वापस नहीं लौटता है
View Solutionएक कण R त्रिज्या के वृत्त की परिधि पर चाल u=2t2 से गति कर रहा है। कॉलम-I में दी गई राशियों को कॉलम-II में दिए गए अनुकूल परिमाणों के साथ सुमेलित कीजिए

View SolutionMatch the columns. M mass and R(lt1) The velocity v of a particle located at a distance r from the center of a homogeneous circular planet of radius is the magnitude of which is given in column i. Match the trajectory from column II about the possible nature of the orbit.
View Solution

