How many n-octene can show geometrical isomerism?
The correct Answer is:3 (oct-2-ene, oct-3-ene, oct-4-ene)
To determine how many n-octenes can show geometrical isomerism, we need to analyze the structures of n-octene and identify the presence of double bonds and substituents around those double bonds.
1. Understanding Geometrical Isomerism:
- Geometrical isomerism occurs in alkenes (compounds with a carbon-carbon double bond) when there are different groups attached to the carbon atoms involved in the double bond.
- For geometrical isomerism to occur, the two groups attached to each carbon of the double bond must be different. This means that if we have a structure like C=C with groups R1, R2 on one carbon and R3, R4 on the other, R1 must not equal R2 and R3 must not equal R4.
2. Identifying the Structure of n-Octene:
- n-Octene has the formula C8H16 and can be represented as CH3(CH2)5CH=CH2.
- It can exist in several structural forms (isomers) depending on the position of the double bond.
3. Analyzing Different Isomers:
- The possible positions for the double bond in n-octene are between the following carbon atoms:
- Between C1 and C2
- Between C2 and C3
- Between C3 and C4
- Between C4 and C5
- Between C5 and C6
- Between C6 and C7
- We will analyze each of these positions to see if they can exhibit geometrical isomerism.
4. Position of the Double Bond:
- 1-Octene (C1=C2): This cannot show geometrical isomerism because both groups on C1 are hydrogen.
- 2-Octene (C2=C3): This can show geometrical isomerism since C2 has CH3 and H, and C3 has H and CH2(CH2)3CH3. This gives rise to cis (same side) and trans (opposite side) isomers.
- 3-Octene (C3=C4): Similar to 2-octene, this can also show geometrical isomerism with different groups on C3 and C4.
- 4-Octene (C4=C5): This can show geometrical isomerism as well.
- 5-Octene (C5=C6): This can also show geometrical isomerism.
- 6-Octene (C6=C7): This cannot show geometrical isomerism because both groups on C6 are hydrogen.
5. Counting the Isomers:
- From the analysis:
- 1-Octene: 0 isomers
- 2-Octene: 2 isomers (cis and trans)
- 3-Octene: 2 isomers (cis and trans)
- 4-Octene: 2 isomers (cis and trans)
- 5-Octene: 2 isomers (cis and trans)
- 6-Octene: 0 isomers
- Total geometrical isomers = 0 + 2 + 2 + 2 + 2 + 0 = 8.
Final Answer:
Thus, the total number of n-octenes that can show geometrical isomerism is 8.
- Geometrical isomerism occurs in alkenes (compounds with a carbon-carbon double bond) when there are different groups attached to the carbon atoms involved in the double bond.
- For geometrical isomerism to occur, the two groups attached to each carbon of the double bond must be different. This means that if we have a structure like C=C with groups R1, R2 on one carbon and R3, R4 on the other, R1 must not equal R2 and R3 must not equal R4.
- n-Octene has the formula C8H16 and can be represented as CH3(CH2)5CH=CH2.
- It can exist in several structural forms (isomers) depending on the position of the double bond.
- The possible positions for the double bond in n-octene are between the following carbon atoms:
- Between C1 and C2
- Between C2 and C3
- Between C3 and C4
- Between C4 and C5
- Between C5 and C6
- Between C6 and C7
- We will analyze each of these positions to see if they can exhibit geometrical isomerism.
- 1-Octene (C1=C2): This cannot show geometrical isomerism because both groups on C1 are hydrogen.
- 2-Octene (C2=C3): This can show geometrical isomerism since C2 has CH3 and H, and C3 has H and CH2(CH2)3CH3. This gives rise to cis (same side) and trans (opposite side) isomers.
- 3-Octene (C3=C4): Similar to 2-octene, this can also show geometrical isomerism with different groups on C3 and C4.
- 4-Octene (C4=C5): This can show geometrical isomerism as well.
- 5-Octene (C5=C6): This can also show geometrical isomerism.
- 6-Octene (C6=C7): This cannot show geometrical isomerism because both groups on C6 are hydrogen.
- From the analysis:
- 1-Octene: 0 isomers
- 2-Octene: 2 isomers (cis and trans)
- 3-Octene: 2 isomers (cis and trans)
- 4-Octene: 2 isomers (cis and trans)
- 5-Octene: 2 isomers (cis and trans)
- 6-Octene: 0 isomers
- Total geometrical isomers = 0 + 2 + 2 + 2 + 2 + 0 = 8.
Thus, the total number of n-octenes that can show geometrical isomerism is 8.
टॉपर्स ने हल किए ये सवाल
- STEREOISOMERISMBook:RESONANCE ENGLISHChapter:STEREOISOMERISMExercise:EXERCISE (PART 1 SECTION (J))
Explore 6 Videos
- STEREOISOMERISMBook:RESONANCE ENGLISHChapter:STEREOISOMERISMExercise:EXERCISE (PART 1 SECTION (K))
Explore 2 Videos
- STEREOISOMERISMBook:RESONANCE ENGLISHChapter:STEREOISOMERISMExercise:EXERCISE (PART 1 SECTION (H))
Explore 2 Videos
- SOLUTIONSBook:RESONANCE ENGLISHChapter:SOLUTIONSExercise:Advabced Level Problems (PART-2)
Explore 35 Videos
- STRUCTURAL IDENTIFICATIONBook:RESONANCE ENGLISHChapter:STRUCTURAL IDENTIFICATIONExercise:Advanced level Problems (Part-III)
Explore 12 Videos
समान प्रश्न
ज्ञान जांच
Which of the following compound can show geometrical isomerism ?
A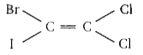 B
B C
C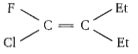 D
D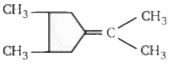
An alcohol X on heating with concentrated H2SO4 gives an alkene Y which can show geometrical isomerism . The alcohol X is
ACH3CH2CH(OH)CH3B(CH3)2C(OH)CH(CH3)2C(CH3)3C(OH)D(CH3)2C(OH)CH2CH3
Can 2-pentene show geometrical isomerism ?
View Solution2-butene shows geometrical isomerism due to:
View Solution2-butene shows geometrical isomerism due to:
View SolutionIn given compounds how many can show geometrical isomerism : ,
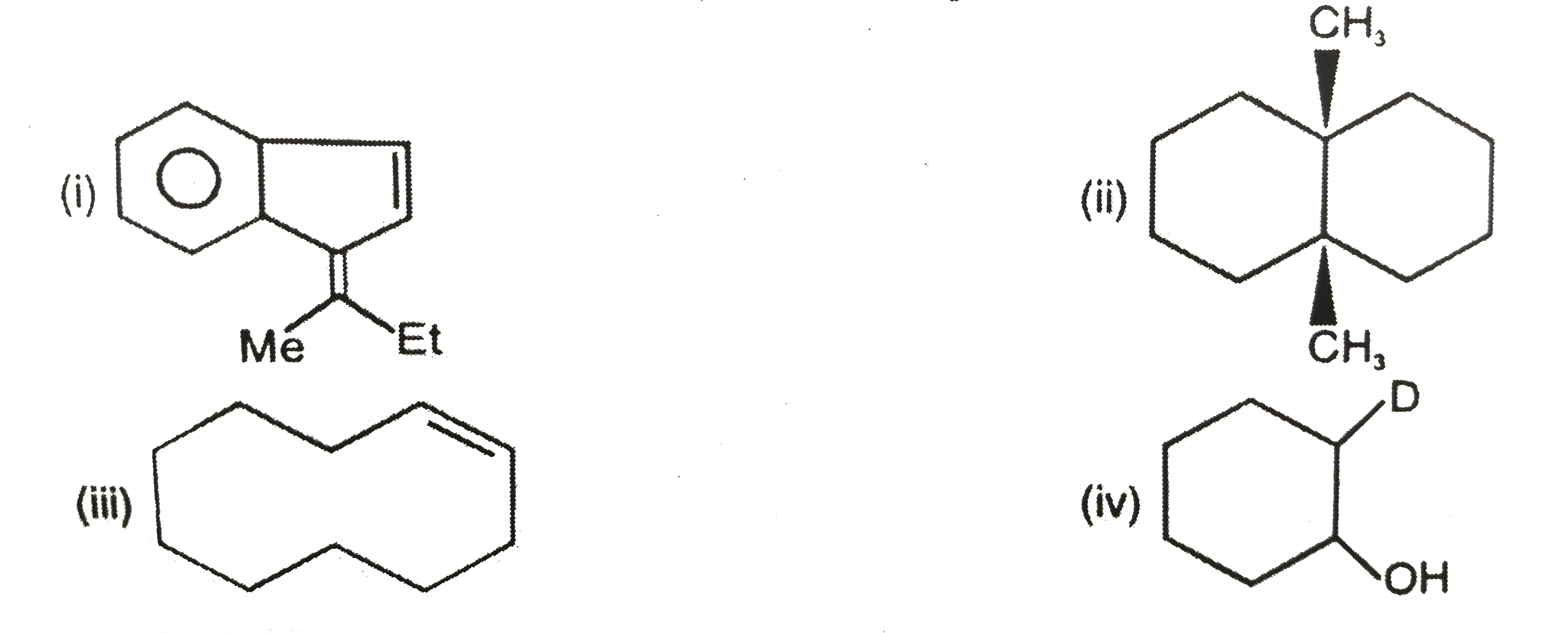
View SolutionHow many of the following can show geometrical isomerism
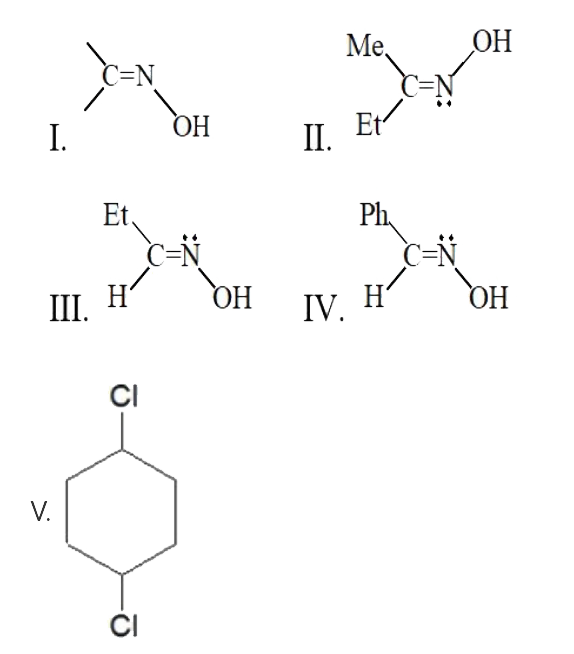
VI. CHCl=C=CHCl
VII. pH−N=N−Ph
VIII. MeCH=N−NH2
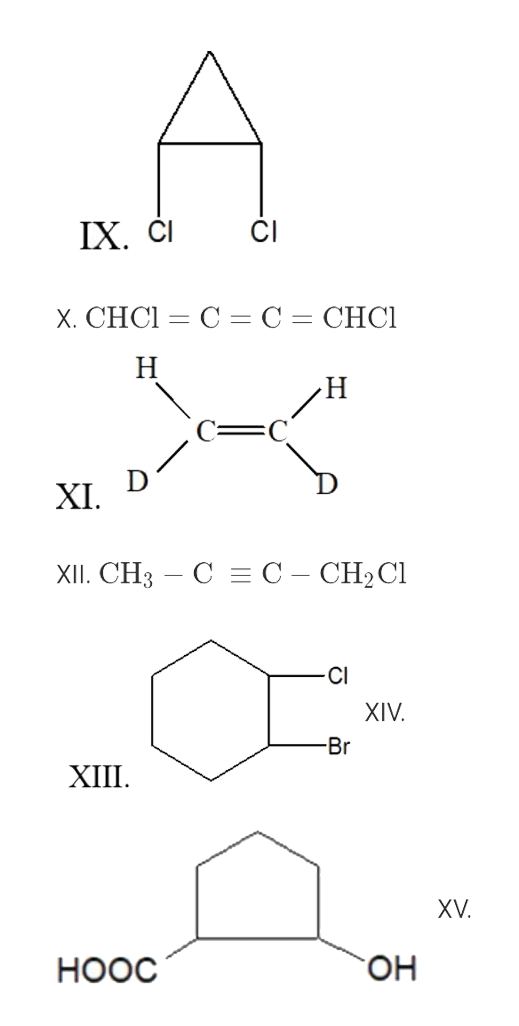

View SolutionWhich of the following can show geometrical isomerism?
(i) Propene (ii) But-1-ene (iii) But-2-ene (iv) Pent-2-ene
View Solution
