(i) CH2=CH−CH2−CH=CH2
(ii) CH2=CH−CH=CH−CH3
(iii) CH3−CH=CH−CH=CH−CH3
The numbers of possible geometrical isomers for the above compounds are
0, 2, 4
2, 2 4
0, 3, 3
0,23
The correct Answer is:D
To determine the number of possible geometrical isomers for the given compounds, we need to analyze each compound based on the conditions for geometrical isomerism. The key conditions are:
1. The compound must be planar (which typically involves sp² hybridized carbon atoms).
2. Each sp² hybridized carbon atom must have different groups attached to it.
Let's analyze each compound step by step:
Compound (i): CH₂=CH−CH₂−CH=CH₂
1. Identify the double bonds: There are two double bonds in this compound.
2. Analyze the first double bond (C1=C2):
- C1 has two hydrogen atoms (H) attached (C1: H₂C).
- C2 has one hydrogen (H) and one carbon (C3) attached (C2: H-CH₂).
- Since C1 has two identical groups (H), it cannot exhibit geometrical isomerism.
3. Analyze the second double bond (C4=C5):
- C4 has one hydrogen (H) and one carbon (C3) attached (C4: H-CH).
- C5 has two hydrogen atoms (H) attached (C5: H₂C).
- Again, C5 has two identical groups (H), so this double bond cannot exhibit geometrical isomerism.
4. Conclusion: There are 0 geometrical isomers for this compound.
Compound (ii): CH₂=CH−CH=CH−CH₃
1. Identify the double bonds: There are two double bonds in this compound.
2. Analyze the first double bond (C1=C2):
- C1 has two hydrogen atoms (H) attached (C1: H₂C).
- C2 has one hydrogen (H) and one carbon (C3) attached (C2: H-CH).
- C1 has two identical groups (H), so it cannot exhibit geometrical isomerism.
3. Analyze the second double bond (C3=C4):
- C3 has one hydrogen (H) and one carbon (C2) attached (C3: H-CH).
- C4 has one hydrogen (H) and one methyl group (C5: CH₃).
- Since both C3 and C4 have different groups, this double bond can exhibit geometrical isomerism (cis and trans).
4. Conclusion: There are 2 geometrical isomers (cis and trans) for this compound.
Compound (iii): CH₃−CH=CH−CH=CH−CH₃
1. Identify the double bonds: There are two double bonds in this compound.
2. Analyze the first double bond (C2=C3):
- C2 has one hydrogen (H) and one carbon (C1) attached (C2: H-CH).
- C3 has one hydrogen (H) and one carbon (C4) attached (C3: H-CH).
- Both C2 and C3 have different groups, so this double bond can exhibit geometrical isomerism (cis and trans).
3. Analyze the second double bond (C4=C5):
- C4 has one hydrogen (H) and one carbon (C3) attached (C4: H-CH).
- C5 has one hydrogen (H) and one carbon (C6) attached (C5: H-CH).
- Again, both C4 and C5 have different groups, so this double bond can exhibit geometrical isomerism (cis and trans).
4. Conclusion: There are 4 geometrical isomers (cis and trans for each double bond).
Summary of Results:
- Compound (i): 0 geometrical isomers
- Compound (ii): 2 geometrical isomers
- Compound (iii): 4 geometrical isomers
Final Answer:
The total number of possible geometrical isomers for the three compounds is:
- 0 + 2 + 4 = 6 geometrical isomers.
2. Each sp² hybridized carbon atom must have different groups attached to it.
2. Analyze the first double bond (C1=C2):
- C1 has two hydrogen atoms (H) attached (C1: H₂C).
- C2 has one hydrogen (H) and one carbon (C3) attached (C2: H-CH₂).
- Since C1 has two identical groups (H), it cannot exhibit geometrical isomerism.
3. Analyze the second double bond (C4=C5):
- C4 has one hydrogen (H) and one carbon (C3) attached (C4: H-CH).
- C5 has two hydrogen atoms (H) attached (C5: H₂C).
- Again, C5 has two identical groups (H), so this double bond cannot exhibit geometrical isomerism.
4. Conclusion: There are 0 geometrical isomers for this compound.
2. Analyze the first double bond (C1=C2):
- C1 has two hydrogen atoms (H) attached (C1: H₂C).
- C2 has one hydrogen (H) and one carbon (C3) attached (C2: H-CH).
- C1 has two identical groups (H), so it cannot exhibit geometrical isomerism.
3. Analyze the second double bond (C3=C4):
- C3 has one hydrogen (H) and one carbon (C2) attached (C3: H-CH).
- C4 has one hydrogen (H) and one methyl group (C5: CH₃).
- Since both C3 and C4 have different groups, this double bond can exhibit geometrical isomerism (cis and trans).
4. Conclusion: There are 2 geometrical isomers (cis and trans) for this compound.
2. Analyze the first double bond (C2=C3):
- C2 has one hydrogen (H) and one carbon (C1) attached (C2: H-CH).
- C3 has one hydrogen (H) and one carbon (C4) attached (C3: H-CH).
- Both C2 and C3 have different groups, so this double bond can exhibit geometrical isomerism (cis and trans).
3. Analyze the second double bond (C4=C5):
- C4 has one hydrogen (H) and one carbon (C3) attached (C4: H-CH).
- C5 has one hydrogen (H) and one carbon (C6) attached (C5: H-CH).
- Again, both C4 and C5 have different groups, so this double bond can exhibit geometrical isomerism (cis and trans).
4. Conclusion: There are 4 geometrical isomers (cis and trans for each double bond).
- Compound (i): 0 geometrical isomers
- Compound (ii): 2 geometrical isomers
- Compound (iii): 4 geometrical isomers
The total number of possible geometrical isomers for the three compounds is:
- 0 + 2 + 4 = 6 geometrical isomers.
Topper's Solved these Questions
- STEREOISOMERISMBook:RESONANCE ENGLISHChapter:STEREOISOMERISMExercise:EXERCISE (PART III : PRACTICE TEST-2 (IIT-JEE (ADVANCED PATTERN))
Explore 23 Videos
- STEREOISOMERISMBook:RESONANCE ENGLISHChapter:STEREOISOMERISMExercise:EXERCISE (ADDITIONAL PROBLEMS FOR SELF PRACTICE (APSP)) PART 1
Explore 30 Videos
- SOLUTIONSBook:RESONANCE ENGLISHChapter:SOLUTIONSExercise:Advabced Level Problems (PART-2)
Explore 35 Videos
- STRUCTURAL IDENTIFICATIONBook:RESONANCE ENGLISHChapter:STRUCTURAL IDENTIFICATIONExercise:Advanced level Problems (Part-III)
Explore 12 Videos
Similar Questions
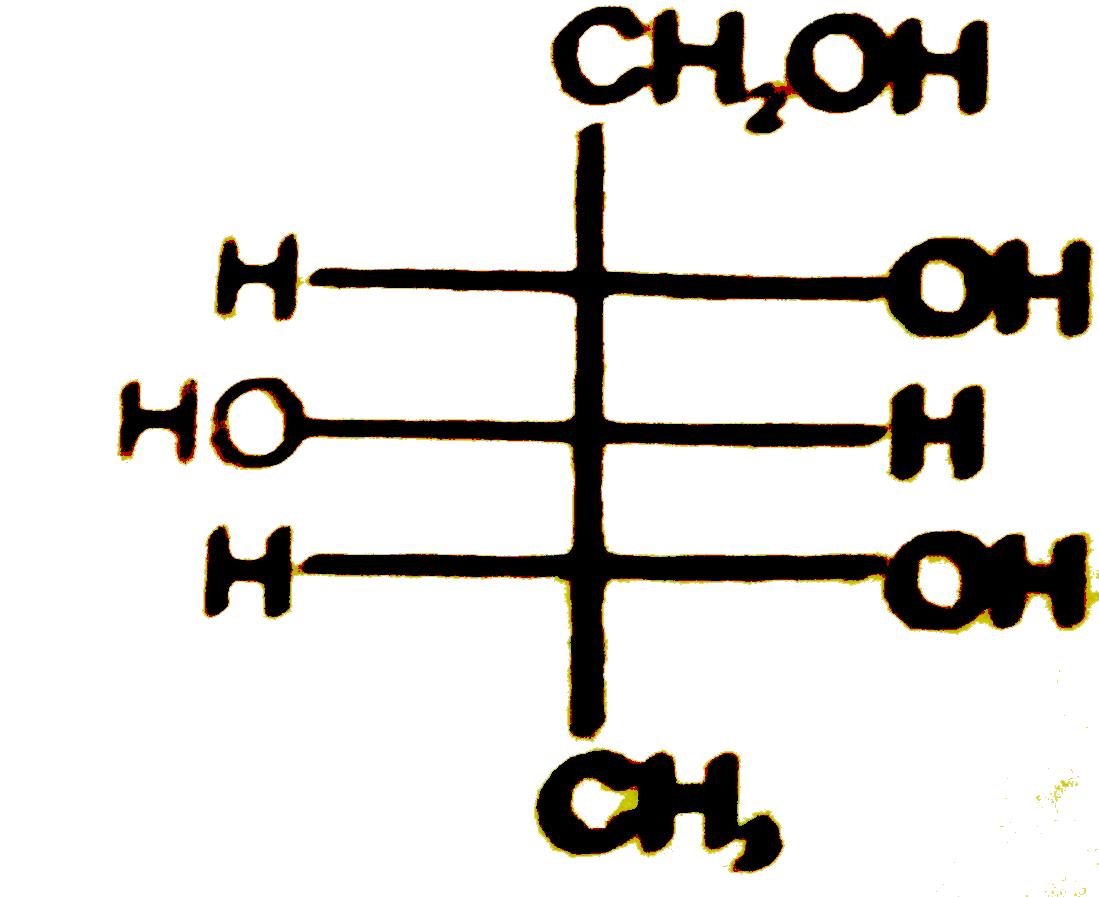 is a Fischer projection of one of_______ stereoisomers ?
is a Fischer projection of one of_______ stereoisomers ?
View SolutionWhich is the pair of geometrical isomers :

View SolutionThe osmotic pressure of 6% solution of urea at 300 K is
View SolutionWhat simple laboratory test could be performed to distinguish between 1-pentyne and 2-pentyne?
View SolutionThe number of geometrical isomers for CH_(3)-CH=CH-CH=CH-CH=CH_(2) is
View SolutionThe following two isomeric alkenes are related as−
(I) CH3−CH=CH−CH2−CH2−CH3
(II) CH3−CH2−CH=CH−CH2−CH3
View SolutionMe (CH=CH-CH=C=CH-CH=CH_(2) Total number of geometrical isomers possible for above compound are:
View SolutionIUPAC name is CH3−CH=CH−CH=CH2
View SolutionCH2=CH−CH=CH−CH=CH2
How many geometrical isomers ar possible for this compound ?
View SolutionCH3−Ch=CH−CH=CH−CH−CH3, total number of geometrical isomer is :
View SolutionGive the IUPAC names of the following :
(i) CH3−CH=CH−CH=CH2
(ii) CH3−CH2−CHO
(iii) CH−O∣∣C−CH2−CH3
View SolutionGive the IUPAC names of the following compounds : (i) {:(" "CH_(2)OH),(" |"),(CH_(3)-CH_(2)-CH-CH-CH-CH_(3)),(" |"" |"),(" "CH_(2)Cl" "CH_(3)):} (ii) {:(" "CH_(2)OH),(" |"),(CH_(3)-CH-CH_(2)-CH-CH-CH_(3)),(" |"" |"),(" "CH_(3)" "OH):} (iii) H_(2)C=CH-underset(OH)underset(|)(CH)-CH_(2)-CH_(2)-CH_(3) (iv)
View SolutionHow much geometrical isomers are possible for the given compound?
CH3−CH=CH−CH=CH−CH=CH2
View Solution(i) CH_(2)=CH-CH_(2)-CH=CH_(2) (ii) CH_(2)=CH-CH=CH-CH_(3) (iii) CH_(3)-CH=CH-CH=CH-CH_(3) The numbers of possible geometrical isomers for the above compounds are
View SolutionHow many geometrical isomers are possible in the following two alkenes?
(i) CH3−CH=CH−CH=CH−CH3
CH3−CH=CH−CH=CH−Cl
View SolutionCH3CH2CH=CH2 and CH3CH=CH−CH3 show
View Solution
