A={1,2,3,...,9}. If three numbers are selected from set A and are arranged, the probability that three numbers are either in increasing order or in decreasing order.
16
23
12
13
The correct Answer is:D
To solve the problem, we need to find the probability that three numbers selected from the set A={1,2,3,…,9} are arranged in either increasing or decreasing order.
1. Determine the Total Ways to Select and Arrange 3 Numbers:
- First, we need to select 3 numbers from the set of 9. The number of ways to choose 3 numbers from 9 is given by the combination formula:
(nr)=n!r!(n−r)!
Here, n=9 and r=3:
(93)=9!3!(9−3)!=9×8×73×2×1=84
2. Calculate the Arrangements of the Selected Numbers:
- Once we have selected 3 numbers, we can arrange them in 3! (factorial of 3) ways:
3!=6
- Therefore, the total number of arrangements of any 3 selected numbers is:
Total arrangements=(93)×3!=84×6=504
3. Determine the Favorable Outcomes (Increasing or Decreasing Order):
- For any set of 3 distinct numbers, there are exactly 2 arrangements that are either in increasing order or in decreasing order. For example, if we select the numbers 1, 2, and 3, they can be arranged as:
- Increasing: 1,2,3
- Decreasing: 3,2,1
- Hence, the total number of favorable outcomes is:
Favorable outcomes=(93)×2=84×2=168
4. Calculate the Probability:
- The probability P that the three selected numbers are either in increasing or decreasing order is given by the ratio of the number of favorable outcomes to the total arrangements:
P=Favorable outcomesTotal arrangements=168504
- Simplifying this fraction:
P=168÷168504÷168=13
Final Answer:
The probability that three numbers selected from set A are either in increasing order or in decreasing order is 13.
- First, we need to select 3 numbers from the set of 9. The number of ways to choose 3 numbers from 9 is given by the combination formula:
(nr)=n!r!(n−r)!
Here, n=9 and r=3:
(93)=9!3!(9−3)!=9×8×73×2×1=84
- Once we have selected 3 numbers, we can arrange them in 3! (factorial of 3) ways:
3!=6
- Therefore, the total number of arrangements of any 3 selected numbers is:
Total arrangements=(93)×3!=84×6=504
- For any set of 3 distinct numbers, there are exactly 2 arrangements that are either in increasing order or in decreasing order. For example, if we select the numbers 1, 2, and 3, they can be arranged as:
- Increasing: 1,2,3
- Decreasing: 3,2,1
- Hence, the total number of favorable outcomes is:
Favorable outcomes=(93)×2=84×2=168
- The probability P that the three selected numbers are either in increasing or decreasing order is given by the ratio of the number of favorable outcomes to the total arrangements:
P=Favorable outcomesTotal arrangements=168504
- Simplifying this fraction:
P=168÷168504÷168=13
The probability that three numbers selected from set A are either in increasing order or in decreasing order is 13.
Topper's Solved these Questions
- TEST PAPERBook:RESONANCE ENGLISHChapter:TEST PAPERExercise:PHYSICS
Explore 14 Videos
- TEST PAPERBook:RESONANCE ENGLISHChapter:TEST PAPERExercise:CHEMISTRY
Explore 1 Video
- SEQUENCE & SERIES Book:RESONANCE ENGLISHChapter:SEQUENCE & SERIES Exercise:EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)
Explore 3 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:MATHEMATICS
Explore 257 Videos
Similar Questions
Knowledge Check
Three numbers are chosen at random from 1 to 20 .The probability that they are consecutive is
A1190B1120C3190D5190Arrange the following in decreasing order of E2 reaction :
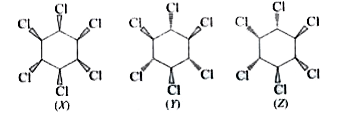 AX>Y>ZBX>Z>YCZ>X>YDY>X>Z
AX>Y>ZBX>Z>YCZ>X>YDY>X>ZArrange the following in decreasing order of E2 reaction :
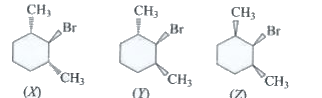 AX>Y>ZBX>Z>YCY>Z>XDZ>Y>X
AX>Y>ZBX>Z>YCY>Z>XDZ>Y>X
Three numbers are chosen at random from numbers 1 to 30. Write the probability that the chosen number are consecutive.
View SolutionNumber of leucocytes in decreasing order in human blood is
View SolutionThree distinct number are selected from first 100 natural numbers. The probability that all the numbers are divisible by 2 and 3 is _________
View SolutionThree numbers are chosen from 1 to 30. The probability that they are not consecutive is
View SolutionThree dice are thrown together. The probability that the sum of the numbers appearing on them is 9, is
View Solution
