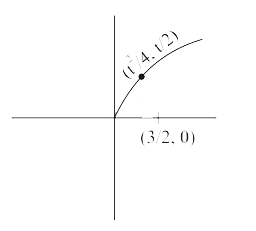
The shortest distance between the point (32,0) and the curve y=√x,(x>0)is
The correct Answer is:5
The point located nearest to the given point must be the point common to the parabola and the normal passing through (32,0).
t2t24−32=−t
2tt2−6+t=0
t(2t2−6+1)=0
t2−6=−2
t2=4
t=2 (t>0)
Point (1,1)
Distance =√(1−32)2+1=√52
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 29 (2020)Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 29 (2020)Exercise:MATHEMATICS
Explore 25 Videos
- JEE MAIN REVISION TEST - 7|JEE - 2020Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 7|JEE - 2020Exercise:Mathematics (Section - 2) Numercial type questions
Explore 5 Videos
Similar Questions
(~(p∨q))∨(~p∧q) is logically equivalent to
View SolutionIn a class of 60 students, 40 opted for NCC, 30 opted for NSS and 20 opted for both NCC and NSS. If one of these students is selected at random, then the probability that the student selected has opted neither for NCC nor for NSS is
View SolutionFind the shortest distance between the curves y2=x3and 9x2+9y2−30y+16=0
View SolutionThe shortest distance between the curve y=x^(2)+7x+2 and the line y=3x-3 is
View SolutionFind the shortest distance between the line x-y+1=0 and the curve y^(2)=x
View SolutionThe shortest distance between curves y2=8x and y2=4(x−3) is
View SolutionThe shortest distance between the point (32,0) and the curve y=√x,(x>0), is
View SolutionThe shortest distance between the curves y=∣∣x2–6x–27∣∣and(x–3)2+(y–39)2=4 is
View SolutionThe shortest distance between the point (32,0) and the curve y=√x,(x>0), is √k2. The value of k is ___________.
View SolutionThe shortest distance between the point (0,12) and the curve x=√y,(y>0) , is:
View SolutionThe shortest distance between y−x=1 and curve x=y2 is :
View SolutionThe shortest distance between y−x=1 and curve x=y2 is :
View SolutionThe shortest distance between the point (32,0) and the curve y=√x,(x>0), is
View SolutionThe shortest distance between curves y2=8x and y2=4(x−3) is
View SolutionFind the shortest distance between the line x−y+1=0 and the curve y2=x.
View SolutionThe shortest distance between the point (0,12) and the curve x=√y,(y>0) , is:
View Solution
