If E,M,J,andG , respectively , denote energy , mass , angular momentum , and gravitational constant , then EJ2/M5G2 has the dimensions of
angle
length
mass
time
The correct Answer is:A
To solve the problem, we need to find the dimensions of the expression EJ2M5G2, where E is energy, M is mass, J is angular momentum, and G is the gravitational constant. We will start by writing down the dimensions of each of these quantities.
Step 1: Write down the dimensions of each variable
1. Energy (E): The dimensional formula for energy is given by:
(E)=(M)(L2)(T−2)=ML2T−2
2. Mass (M): The dimensional formula for mass is:
(M)=M
3. Angular Momentum (J): The dimensional formula for angular momentum is:
(J)=(M)(L2)(T−1)=ML2T−1
4. Gravitational Constant (G): The dimensional formula for the gravitational constant is:
(G)=M−1L3T−2
Step 2: Substitute the dimensions into the expression
Now we substitute these dimensions into the expression EJ2M5G2.
EJ2M5G2=(ML2T−2)(ML2T−1)2M5(M−1L3T−2)2
Step 3: Calculate J2 and G2
Calculating J2:
(J2)=(ML2T−1)2=M2L4T−2
Calculating G2:
(G2)=(M−1L3T−2)2=M−2L6T−4
Step 4: Substitute back into the expression
Now substituting J2 and G2 back into the expression:
EJ2M5G2=(ML2T−2)(M2L4T−2)M5(M−2L6T−4)
Step 5: Simplify the expression
Now we simplify the expression step by step:
1. The numerator becomes:
M1+2L2+4T−2−2=M3L6T−4
2. The denominator becomes:
M5(M−2L6T−4)=M5−2L6T−4=M3L6T−4
Now we have:
M3L6T−4M3L6T−4=1
Step 6: Conclusion
The result is dimensionless, which means it has no dimensions. Therefore, the final answer is that the expression EJ2M5G2 is dimensionless.
(E)=(M)(L2)(T−2)=ML2T−2
(M)=M
(J)=(M)(L2)(T−1)=ML2T−1
(G)=M−1L3T−2
(J2)=(ML2T−1)2=M2L4T−2
(G2)=(M−1L3T−2)2=M−2L6T−4
EJ2M5G2=(ML2T−2)(M2L4T−2)M5(M−2L6T−4)
1. The numerator becomes:
M1+2L2+4T−2−2=M3L6T−4
M5(M−2L6T−4)=M5−2L6T−4=M3L6T−4
M3L6T−4M3L6T−4=1
टॉपर्स ने हल किए ये सवाल
- JEE MAIN REVISION TEST - 18Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 18Exercise:PHYSICS - SECTION 2
Explore 5 Videos
- JEE MAIN REVISION TEST - 13Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 13Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST - 19Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 19Exercise:PHYSICS
Explore 25 Videos
समान प्रश्न
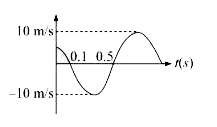
The velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
View SolutionAn insulting thin rod of length l has a linear charge density ρ(x)=ρ0xl on it. The rod is rotated about an axis passing through the origin (x=0) and perpendicular to the rod. If the rod makes n rotations per second, then the time averaged magnetic moment of the rod is :
View SolutionIf E,M,J,andG , respectively , denote energy , mass , angular momentum , and gravitational constant , then EJ2/M5G2 has the dimensions of
View SolutionE, m, L, G denote energy mass, angular momentum & gravitation constant respectively. The dimensions of EL2m5G2 will be that of :
View SolutionIf E,M,J and G respectively denote energy , mass angular momentum and gravitational constant then EJ2M2G2 has the dimensions of .
View SolutionIf E is energy M is mass, J is angular momentum and G is universal gravitational constant ,then dimensions of x=EJ^2/G^2M^5 can be that of
View SolutionIf E, M, J and G respectively denote energy, mass angular momentum and universal gravitational constant, the quantity, which has the same dimensions as the dimensions of (EJ^(2))/(M^(5)G^(2))
View SolutionE,m,L and G denote energy, mass, angular momentum and gravititional constant respectively, the quantity E.Lm5G2 has the dimensions of :
View SolutionIf E, m, J and G are the energy, mass, angular momentum and gravitational constant respectively, then EJ^(2)/m^(5)G^(2) Is the dimensional formula of
View SolutionIf E, m, l and G denote energy, mass, angular momentum and gravitational constant respectively, the quantity (El^(2)//m^(5)G^(2)) has the dimensions of
View SolutionIf E , M , J , and G , respectively , denote energy , mass , angular momentum , and gravitational constant , then EJ^(2) //M^(5) G^(2) has the dimensions of
View SolutionIf E,M,J,andG , respectively , denote energy , mass , angular momentum , and gravitational constant , then EJ2/M5G2 has the dimensions of
View SolutionIf E,M,J and G respectively denote energy , mass angular momentum and gravitational constant then (EJ^(2))/(M^(5)G^(2)) has the dimensions of .
View SolutionIf E, M, J and G denote energy, mass, angular momentum and gravitational constant respectively, calculate the dimensions of the quantity (EJ^(2))/(M^(5)G^(2)) .
View Solution
