The shortest distance from the point (2,-7) to thwe circe x2+y2−14x−10y−151=0 is equal to 5.
1 unit
2 units
3 units
4 units
The correct Answer is:B
Step by step video solution for The shortest distance from the point (2,-7) to thwe circe x^(2)+y^(2)-14x-10y-151=0 is equal to 5. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - VMC MODULES ENGLISHCHAPTER - CIRCLESEXERCISE - LEVEL-2
50 Videos
- CIRCLESBOOK - VMC MODULES ENGLISHCHAPTER - CIRCLESEXERCISE - NUMERICAL VALUE TYPE FOR JEE MAIN
15 Videos
- CIRCLESBOOK - VMC MODULES ENGLISHCHAPTER - CIRCLESEXERCISE - JEE ADVANCED ( ARCHIVE )
68 Videos
- BINOMIAL THEOREMBOOK - VMC MODULES ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - JEE Archive
56 Videos
- COMPLEX NUMBERS BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - JEE ARCHIVE
76 Videos
Similar Questions
Let L1 be a straight line passing through (0,0)andL2 be x+y=1. If the intercepts made by the circel x2+y2−x+3y=0onL1andL2 are equal, then which of the following equations can represent L1?
View SolutionIf P(2,8) is an interior point of a circle x2+y2−2x+4y−λ=0 which neither touches nor intersects the axes, then set for λ is
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle. Then a) the area of ABC is maximum when it is isosceles b) the area of ABC is minimum when it is isosceles c) the perimeter of ABC is minimum when it is isosceles d) none of these
View SolutionThe sum of coefficient of integral powers of x in the binomial expansion of (1−2√x)50 is
View SolutionA complex number z is said to be unimodular if |z|=1. Suppose z1 and z2 are complex numbers such that z1−2z22−z1z_2 is unimodular and z2 is not unimodular. Then the point z1 lies on a
View SolutionFind the shortest distance from the point M(-7,2) to the circle x^(2)+y^(2)-10x-14y-151=0
View Solution. The shortest distance from the point (2,-7) to circle x^(2)+y^(2)-14x-10y-151=0
View SolutionThe sum of the minimum distance and the maximum distance from the point (2,2) to the circle x^(2)+y^(2)+4x-10y-7=0 is
View SolutionThe shortest distance from the point (0,5) to the circumference of the circle x2+y2−10x+14y−151=0 is: (A) 13 (B) 9 (C) 2 (D) 5
View SolutionThe shortest distance form the point P(−7,2) to the cirlce x2+y2−10x−14y−151=0 in units
View SolutionThe shortest distance of the point (1, 3, 5) from
x2+y2=0 is
View Solutionबिन्दु (2, -7) से वृत्त x2+y2−14x−10y−151=0 का न्यूनतम दूरी है:
View Solutionपरवलय y=x2 से बिंदु (0,a) कि न्यूनतम दूरी ज्ञात कीजिए।
View SolutionCompute the shortest distance between the circle x2+y2−10x−14y−151=0 and the point (−7,2).
View Solutionx2+y2−14x−10y+24=0 makes an
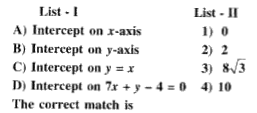
View Solution. The shortest distance from the point (2, -7) to circle x2+y2−14x−10y−151=0
View Solution

