Discuss the differentiability of f(x)=[x]+√{x}), where [.] and {.} denote the greatest integer function and fractional part repectively .
contiunous but non-differentiable at x=1
differentiable at x=1
discontinuous at x=1
None of these
The correct Answer is:A
Step by step video solution for Discuss the differentiability of f(x) =[x]+ sqrt({x})), where [.] and {.} denote the greatest integer function and fractional part repectively . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUSBook:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUSExercise:LEVEL 2
Explore 103 Videos
- DIFFERENTIAL CALCULUSBook:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUSExercise:Numerical Value Type for JEE Main
Explore 14 Videos
- DIFFERENTIAL CALCULUSBook:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUSExercise:JEE Advanced (Archive)
Explore 75 Videos
- CONIC SECTIONSBook:VMC MODULES ENGLISHChapter:CONIC SECTIONSExercise:JEE ADVANCED ARCHIVE
Explore 76 Videos
- DIFFERENTIAL CALCULUS 2Book:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUS 2Exercise:JEE Advanced (Archive)
Explore 81 Videos
Similar Questions
If limx→∞(x2+1x+1−ax−b)=0, find the values of a and b.
View SolutionIf f and g are two functions having derivative of order three for all x satisfying f(x)g(x)=C (constant) and f'''f'−Af''f−g'''g'+3gg=0. Then A is equal to
View SolutionLet g:R→R be a differentiable function with g(0)=0,,g'(1)≠0.Let f(x)={x|x|g(x),0≠0and0,x=0 and h(x)=e|x| for all x∈R. Let (foh)(x) denote f(h(x))and(hof)(x) denote h(f(x)). Then which of the following is (are) true?
A. f is differentiable at x = 0
B. h is differentiable at x = 0
C. f o h is differentiable at x = 0
D. h o f is differentiable at x = 0
View SolutionThe axis of a parabola is along the line y=x and the distance of its vertex and focus from the origin are √2 and 2√2 , respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is
(a) (x+y)2=(x−y−2) (b)(x−y)2=(x+y−2) (c)(x−y)2=4(x+y−2) (d)(x−y)2=8(x+y−2)
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:
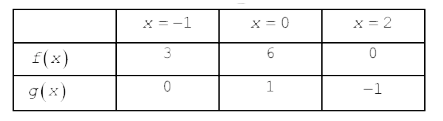
In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View SolutionIf [.] denotes the greatest integer function and {.} denotes the fractional part,then the domain of the function f(x)=sqrt((x-1)/(x-{x}))+ln(3-[x+[2x]]) is
View SolutionThe range of function f(x)=log_(x)([x]), where [.] and {.} denotes greatest integer and fractional part function respectively
View SolutionIf f(x)=[x^(2)]+sqrt({x}^(2)), where [] and {.} denote the greatest integer and fractional part functions respectively,then
View SolutionThe function f(x)=[x]+sqrt({x}), where [.] denotes the greatest Integer function and {.} denotes the fractional part function respectively,is discontinuous at
View SolutionNumber of points of discontinuity of f(x)={(x)/(5)}+{(x)/(2)} in x in[0,100] is/are (where [-] denotes greatest integer function and {:} denotes fractional part function)
View SolutionIf F(x)=sinπ[x]{x} then F(x) is (where {.} denotes fractional part function and [.] denotes greatest integer function and sgn(x) is a signum function)
View SolutionSolve : 4{x}=x+[x](where [⋅] denotes the greatest integer function and {⋅} denotes the fractional part function.
View SolutionThe function f(x)={x}sin(π[x]), where [.] denotes the greatest integer function and {.} is the fraction part function , is discontinuous at
View Solutionf(x)=[x2]−{x}2, where [.] and {.} denote the greatest integer function and the fractional part function , respectively , is
View SolutionThe function f(x)={x}sin(π[x]), where [.] denotes the greatest integer function and {.} is the fractional part function, is discontinuous at
View SolutionSolve : 4{x}=x+[x](where [⋅] denotes the greatest integer function and {⋅} denotes the fractional part function.
View Solution
