d2xdy2 equals: (d2ydx2)−1 (b) −(d2ydx2)−1(dydx)−3 (d2ydx2)(dydx)−2 (d) −(d2ydx2)(dydx)−3
(d2ydx2)−1
−(d2ydx2)−1(dydx)−3
(d2ydx2)(dydx)−2
−(d2ydx2)(dydx)−3
The correct Answer is:D
Step by step video solution for (d^2x)/(dy^2) equals: ((d^2y)/(dx^2))^(-1) (b) -((d^2y)/(dx^2))^(-1)((dy)/(dx))^(-3) ((d^2y)/(dx^2))((dy)/(dx))^(-2) (d) -((d^2y)/(dx^2))((dy)/(dx))^(-3) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE main (Archive)
51 Videos
- CONIC SECTIONSBOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - JEE ADVANCED ARCHIVE
76 Videos
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Advanced (Archive)
81 Videos
Similar Questions
limx→0(1−cosx)(3+cosx)xtan4x is equal to
View SolutionThe axis of a parabola is along the line y=x and the distance of its vertex and focus from the origin are √2 and 2√2 , respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is
(a) (x+y)2=(x−y−2) (b)(x−y)2=(x+y−2) (c)(x−y)2=4(x+y−2) (d)(x−y)2=8(x+y−2)
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:
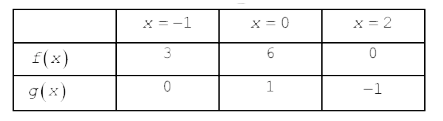
In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View SolutionIn which of the following differential equation degree is not defined? (a)d2ydx2+3(dydx)2=xlog(d2ydx2) (b)(d2ydx2)2+(dydx)2=xsin(d2ydx2) (c)x=sin((dydx)−2y),|x|<1 (d)x−2y=log(dydx)
View SolutionIf R=[1+(dydx)2]3/2d2ydx2 , thenR2/3 can be put in the form of 1(d2ydx2)2/3+1(d2xdy2)2/3 b. 1(d2ydx2)2/3−1(d2xdy2)2/3 c. 2(d2ydx2)2/3+2(d2xdy2)2/3 d. 1(d2ydx2)2/3.1(d2xdy2)2/3
View SolutionFind the order and degree of d2ydx2+3dydx=ysin(d2ydx2)
View Solution(d2ydx2)2+d2ydx2−(dydx)4+dydx+y=6x3 অবকল সমীকরণের মাত্রা-
View Solutiond2xdy2 equals: (1) (d2ydx2)−1 (2) −(d2ydx2)−1(dydx)−3 (3) −(d2ydx2)−1(dydx)−2 (4) −(d2ydx2)−1(dydx)3
View SolutionIf x=logp and y=1p ,then (a)d2ydx2−2p=0 (b) d2ydx2+y=0 (c)d2ydx2+dydx=0 (d) d2ydx2−dydx=0
View Solutiond2xdy2 equals: (1) (d2ydx2)−1 (2) −(d2ydx2)−1(dydx)−3 (3) (d2ydx2)−1(dydx)−2 (4) −(d2ydx2)−1(dydx)−3
View SolutionIf R=[1+(dydx)2]3/2d2ydx2 , thenR2/3 can be put in the form of a. 1(d2ydx2)2/3+1(d2xdy2)2/3 b. 1(d2ydx2)2/3−1(d2xdy2)2/3 c. 2(d2ydx2)2/3+2(d2xdy2)2/3 d. 1(d2ydx2)2/31(d2xdy2)2/3
View SolutionIf R=[1+(dydx)2]−3/2d2ydx2 , thenR2/3 can be put in the form of 1(d2ydx2)2/3+1(d2xdy2)2/3 b. 1(d2ydx2)2/3−1(d2xdy2)2/3 c. 2(d2ydx2)2/3+2(d2xdy2)2/3 d. 1(d2ydx2)2/3.1(d2xdy2)2/3
View Solutiond2xdy2 equals:
(1.) (d2ydx2)−1
(2) −(d2ydx2)(dydx)−3
(3) −(d2ydx2)−1(dydx)−2
(4) −(d2ydx2)−1(dydx)3
View SolutionIf dydx=1dxdy , Show that d2ydx2=−d2xdy2(dxdy)3
View SolutionIf d2xdy2(dydx)3+d2ydx2=Kthen the value of k is equal to
View SolutionFind the order and degree of d2ydx2+3dydx=ysin(d2ydx2)
View Solution

