If =ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1, prove that y'y=1x(aa−x+bb−x+cc−x).
Step by step video solution for "If "=(ax^(2))/((x-a)(x-b)(x-c))+(bx)/((x-b)(x-c))+(c)/(x-c)+1," prove that "(y')/(y)=(1)/(x)((a)/(a-x)+(b)/(b-x)+(c)/(c-x)). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUSBook:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUSExercise:JEE main (Archive)
Explore 51 Videos
- CONIC SECTIONSBook:VMC MODULES ENGLISHChapter:CONIC SECTIONSExercise:JEE ADVANCED ARCHIVE
Explore 76 Videos
- DIFFERENTIAL CALCULUS 2Book:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUS 2Exercise:JEE Advanced (Archive)
Explore 81 Videos
Similar Questions
limx→0(1−cosx)(3+cosx)xtan4x is equal to
View SolutionThe axis of a parabola is along the line y=x and the distance of its vertex and focus from the origin are √2 and 2√2 , respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is
(a) (x+y)2=(x−y−2) (b)(x−y)2=(x+y−2) (c)(x−y)2=4(x+y−2) (d)(x−y)2=8(x+y−2)
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:
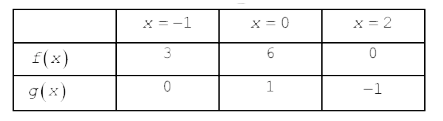
In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View SolutionIf y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1 find dydx
View SolutionProve that: (xaxb)c× (xbxc)a × (xcxa)b=1
View SolutionIf y=(ax^(2))/((x-a)(x-b)(x-c))+(bx)/((x-b)(x-c))+(c)/(x-c)+1 then (y')/(y)=
View SolutionIf y=(ax^(2))/((x-a)(x-b)(x-c))+(bx)/((x-b)(x-c))+(c)/(x-c)+1 then prove that (y')/(y)=(1)/(x)[(a)/(a-x)+(b)/(b-x)+(c)/(c-x)]
View SolutionProve that
ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1
=x3(x−a)(x−b)(x−c).
View SolutionProve that.
(i) √x−1y.√y−1z.Sqrt(z−1x)=1
(ii) (1xa−b)1a−c.(1xb−c).(1xc−b)1c−b=1
(iii) xa(b−c)xb(a−c)÷(xbxa) (iv) (xa+b)2(xb+c)2(xc+a)2(xaxbxc)4
View Solutionयदि y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+c(x−c)+1, तब सिद्ध कीजिएः की dydx=yx(aa−x+bb−x+cc−x)
View SolutionIf y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1, prove that dydx=yx[aa−x+bb−x+cc−x]
View Solutionयदि y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1 है तो सिद्ध कीजिए की dydx=y−x[ax−a+bx−b+cx−c]
View Solutiony=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1 হলে প্রমাণ করো যে, dydx=yx[aa−x+bb−x+cc−x]
View SolutionIf y=(ax^(2))/((x-a)(x-b)(x-c))+(bx)/((x-b)(x-c))+(c)/((x-c))+1 Prove that (y')/(y) =(1)/(x) ((a)/((a-x))+(b)/((b-x))+(c)/((c-x)))
View SolutionIf y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1, then prove that y'y=1x[aa−x+bb−x+cc−x]
View SolutionIf y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1, then prove that y'y=1x[aa−x+bb−x+cc−x]
View Solution
