about to only mathematics
15
16
17
18
The correct Answer is:D
Step by step video solution for about to only mathematics by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUS 2Book:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUS 2Exercise:Level -2
Explore 69 Videos
- DIFFERENTIAL CALCULUS 2Book:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUS 2Exercise:Numerical ValueType for JEE Main
Explore 14 Videos
- DIFFERENTIAL CALCULUS 2Book:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUS 2Exercise:JEE Advanced (Archive)
Explore 81 Videos
- DIFFERENTIAL CALCULUSBook:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUSExercise:JEE Advanced (Archive)
Explore 75 Videos
- DIFFERENTIAL EQUATIONSBook:VMC MODULES ENGLISHChapter:DIFFERENTIAL EQUATIONSExercise:JEE ADVANCE (ARCHIVE )
Explore 32 Videos
Similar Questions
The number of values of x where the function f(x)=cosx+cos(√2x) attains its maximum is (a) 0 (b) 1 (c) 2 (d) infinite
View SolutionLet (a,b) be a point on the parabola y=4x−x2 and is the point nearest to the point A(-1,4) Find (a+b).
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:
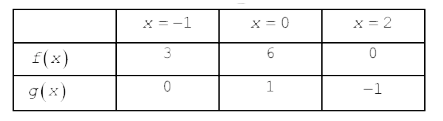
In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View SolutionLet g:R→R be a differentiable function with g(0)=0,,g'(1)≠0.Let f(x)={x|x|g(x),0≠0and0,x=0 and h(x)=e|x| for all x∈R. Let (foh)(x) denote f(h(x))and(hof)(x) denote h(f(x)). Then which of the following is (are) true?
A. f is differentiable at x = 0
B. h is differentiable at x = 0
C. f o h is differentiable at x = 0
D. h o f is differentiable at x = 0
View SolutionThe differential equation dydx=√1−y2y determinea a family of circles with :
View SolutionWhat did Schimba say about mathematics?
View SolutionWhich of the following statements is not true about 'mapping in Mathematics?
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solution
