Tangent lines are drawn at the points P and Q where f''(x) vanishes for the function f(x)=cos x on [0,2π] The tangent lines at P and Q intersect each other at R so as to form a triangle PQR. If area triangle PQR is kπ2 then find the value of 36k.
The correct Answer is:9
To solve the problem step by step, we will follow these instructions:
Step 1: Identify where f′′(x) vanishes
Given the function f(x)=cosx, we need to find the second derivative and determine where it is equal to zero.
1. First, we find the first derivative:
f′(x)=−sinx
2. Next, we find the second derivative:
f′′(x)=−cosx
3. Set the second derivative equal to zero to find the points where it vanishes:
−cosx=0⟹cosx=0
The solutions in the interval (0,2π) are:
x=π2,3π2
Step 2: Find the points P and Q
The points P and Q correspond to x=π2 and x=3π2.
1. Calculate the coordinates of point P:
P=(π2,f(π2))=(π2,0)
2. Calculate the coordinates of point Q:
Q=(3π2,f(3π2))=(3π2,0)
Step 3: Find the equations of the tangent lines at P and Q
1. Calculate the slopes at points P and Q:
- At P:
f′(π2)=−sin(π2)=−1
- At Q:
f′(3π2)=−sin(3π2)=1
2. Write the equation of the tangent line at P:
y−0=−1(x−π2)⟹y=−x+π2
3. Write the equation of the tangent line at Q:
y−0=1(x−3π2)⟹y=x−3π2
Step 4: Find the intersection point R of the tangent lines
Set the equations equal to find R:
−x+π2=x−3π2
Solving for x:
π2+3π2=2x⟹2π=2x⟹x=π
Substituting x=π into one of the tangent equations to find y:
y=−π+π2=−π2
Thus, the coordinates of point R are:
R=(π,−π2)
Step 5: Calculate the area of triangle PQR
The area A of triangle PQR can be calculated using the formula:
A=12×base×height
The base PQ is the distance between P and Q:
PQ=3π2−π2=π
The height is the vertical distance from point R to the line y=0:
height=∣∣∣−π2−0∣∣∣=π2
Thus, the area is:
A=12×π×π2=π24
Step 6: Relate the area to k
According to the problem, the area is given as kπ2:
π24=kπ2⟹k=14
Step 7: Find 36k
Finally, calculate 36k:
36k=36×14=9
Final Answer
Thus, the value of 36k is 9.
---
Given the function f(x)=cosx, we need to find the second derivative and determine where it is equal to zero.
f′(x)=−sinx
f′′(x)=−cosx
−cosx=0⟹cosx=0
The solutions in the interval (0,2π) are:
x=π2,3π2
The points P and Q correspond to x=π2 and x=3π2.
P=(π2,f(π2))=(π2,0)
Q=(3π2,f(3π2))=(3π2,0)
1. Calculate the slopes at points P and Q:
- At P:
f′(π2)=−sin(π2)=−1
- At Q:
f′(3π2)=−sin(3π2)=1
y−0=−1(x−π2)⟹y=−x+π2
y−0=1(x−3π2)⟹y=x−3π2
Set the equations equal to find R:
−x+π2=x−3π2
Solving for x:
π2+3π2=2x⟹2π=2x⟹x=π
Substituting x=π into one of the tangent equations to find y:
y=−π+π2=−π2
Thus, the coordinates of point R are:
R=(π,−π2)
The area A of triangle PQR can be calculated using the formula:
A=12×base×height
The base PQ is the distance between P and Q:
PQ=3π2−π2=π
The height is the vertical distance from point R to the line y=0:
height=∣∣∣−π2−0∣∣∣=π2
Thus, the area is:
A=12×π×π2=π24
According to the problem, the area is given as kπ2:
π24=kπ2⟹k=14
Finally, calculate 36k:
36k=36×14=9
Thus, the value of 36k is 9.
Topper's Solved these Questions
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Main (Archive)
36 Videos
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Advanced (Archive)
81 Videos
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - Level -2
69 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)
75 Videos
- DIFFERENTIAL EQUATIONSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - JEE ADVANCE (ARCHIVE )
32 Videos
Similar Questions
The normal to the curve, x2+2xy−3y2=0,at(1,1)
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:
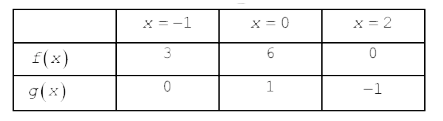
In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View SolutionThe number of values of x where the function f(x)=cosx+cos(√2x) attains its maximum is (a) 0 (b) 1 (c) 2 (d) infinite
View SolutionLet g:R→R be a differentiable function with g(0)=0,,g'(1)≠0.Let f(x)={x|x|g(x),0≠0and0,x=0 and h(x)=e|x| for all x∈R. Let (foh)(x) denote f(h(x))and(hof)(x) denote h(f(x)). Then which of the following is (are) true?
A. f is differentiable at x = 0
B. h is differentiable at x = 0
C. f o h is differentiable at x = 0
D. h o f is differentiable at x = 0
View SolutionThe differential equation dydx=√1−y2y determinea a family of circles with :
View SolutionAn equilateral triangle PQR is formed where P(1,3) is fixed point and Q is moving point on line x=3. Find the locus of R.9.
View SolutionThrough point P(−1,4), two perpendicular lines are drawn which intersect x-axis at Q and R. find the locus of incentre of ΔPQR.
View SolutionLines x + y = 1 and 3y = x + 3 intersect the ellipse x2+9y2=9 at the points P , Q , R . The area of the triangle PQR is _
View SolutionThe tangents to the parabola y2=4ax at P(t1) and Q(t2) intersect at R. The area of Δ PQR is
View SolutionTangent lines are drawn at the points P and Q where f''(x) vanishes for the function f(x)=cos x on [0,2π] The tangent lines at P and Q intersect each other at R so as to form a triangle PQR. If area triangle PQR is kπ2 then find the value of 36k.
View SolutionA point P is given on the circumference of a circle of radius r. The chord QR is parallel to the tangent line at P. Find the maximum area of the triangle PQR.
View Solutionमाना वृत्त x2+y2=9 तथा परवलय y2=8x है। यह प्रथम तथा चतुर्थ चतुर्थाश में क्रमशः P तथा Q पर प्रतिच्छेद करते है। वृत्त की P तथा Q पर स्पर्श रेखाएं x-अक्ष को R पर प्रतिच्छेद करती है तथा परवलय की P तथा Q पर स्पर्श रेखा x-अक्ष को S पर प्रतिच्छेद करती है।
त्रिभुज PQR के अन्तःवृत्त की त्रिज्या है-
View SolutionΔPQR యొక్క అంతరకోణాలు P,Q మరియు R అయిన (tan ( P+Q/2))=
View Solutionযদি PQR একটি পরিবর্তনশীল ত্রিভুজ হয়, তবে cos(P+Q)+cos(Q+R)+cos(R+P) এর সর্বনিম্ন মান হবে–
View Solutionमाना वृत्त x2+y2=9 तथा परवलय y2=8x है। यह प्रथम तथा चतुर्थ चतुर्थाश में क्रमशः P तथा Q पर प्रतिच्छेद करते है। वृत्त की P तथा Q पर स्पर्श रेखाएं x-अक्ष को R पर प्रतिच्छेद करती है तथा परवलय की P तथा Q पर स्पर्श रेखा x-अक्ष को S पर प्रतिच्छेद करती है।
त्रिभुज PRS के परिवृत्त की त्रिज्या है-
View Solution

