A and B are moving in two circular orbits with angular velocity
2ωandω respectively. Their position are shown at t = 0. Find the time at which they will meet for 1st time
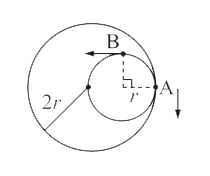
π2ω
3π2ω
πω
They will never meet
The correct Answer is:D
They can meet only at the initial position of A.
time after which A reach this position =πω,2πω,3πω,....=nπω
time after which B reach this position =3π2ω+n2πω
They will never be able to meet as for no value of and these two terms will be same.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
Two discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then

View SolutionA particle moves in a circular path of radius R with an angualr velocity ω=a−bt, where a and b are positive constants and t is time. The magnitude of the acceleration of the particle after time 2ab is
View SolutionA body of mass m is moving in a circle of radius angular velocity ω. Find the expression for centripetal force acting on it by the method of dimensions
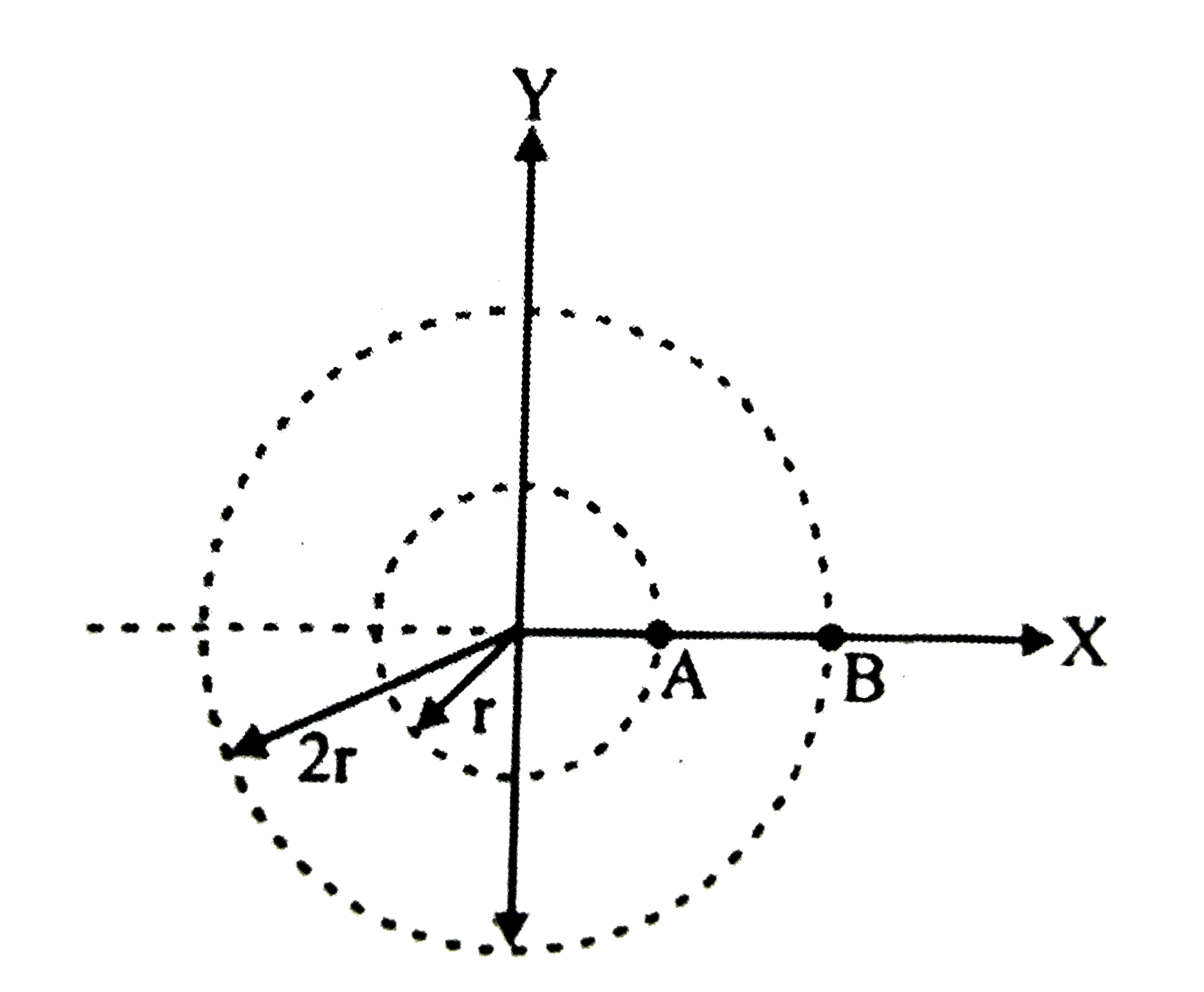
View SolutionTwo particles A and B are moving in a horizontal plane anitclockwise on two different concentric circles with different constant angular velocities 2ω and ω respectively. Find the relative velocity (in m/s) of B w.r.t. A after tome t=π/ω. They both start at the position as shown in figure (Takeω=3rad/sec,r=2m)
View SolutionA conical pendulum is moving in a circle with angular velocity ω as shown. If tension in the string is T, which of following equations are correct ?

View SolutionA partical excutes SHM with amplitudeA and angular frequency ω. At an instant the particle is at a distance A/5 from the mean position and is moving away from it. Find the time after which it will come back to this position again and also find the time after which it will pass through the mean position.
View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View SolutionA uniform rod is hinged at its one end and is allowed to rotate in verticle plANE. Rod is given angular velocity ω in its verticle position as shown in figure. The value of ω for the force exerted by the hinge on rod is zero in this position is

View SolutionA point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant λ.
The magnitude of the induced electric field in the orbit at any instant of time during the time interval of the mangnetic field change is
View SolutionA point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant λ.
The magnitude of the induced electric field in the orbit at any instant of time during the time interval of the mangnetic field change is
View Solution
