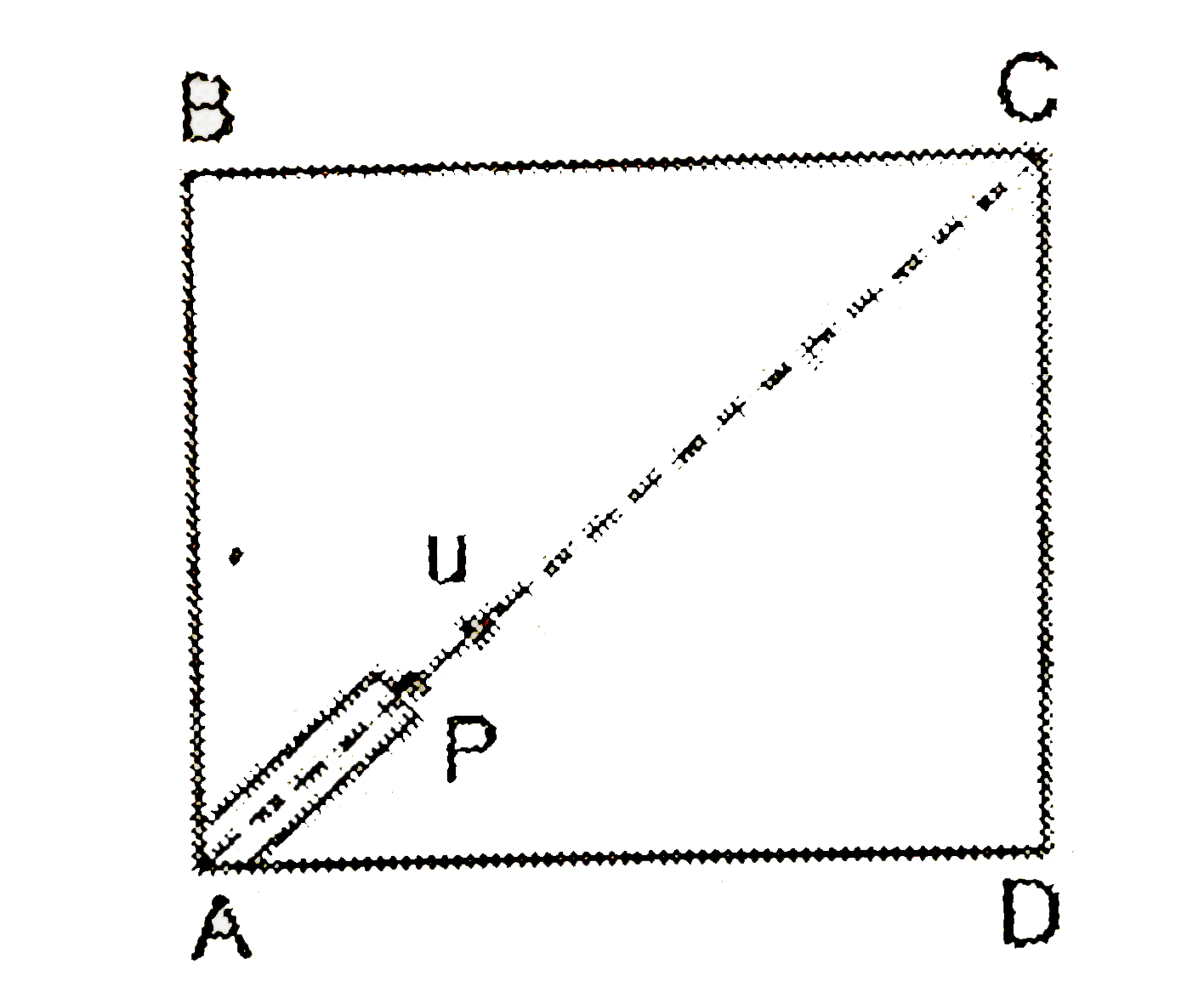
A large rectangular box ABCD falls vertically with an acceleration a. a toy gun fixed at A and aimed towards C fired a particle P.
(a)P will hit C if a = g
(b)P will hit the roof BC if a>g
(c)P will hit the wall CD or the floor AD if a<g
(d)May be either (A), (B) or (C), depending on the speed of projection of P
The correct Answer is:A, B, C
If the relative acceleration of bullet w.r.t. box is zero then its motion is straight line w.r.t. box vertical displacement will be different if a≠g.
टॉपर्स ने हल किए ये सवाल
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
समान प्रश्न
A large rectangular box moves vertically downward with an acceleration a. A toy gun fixed at A and aimed towards C fires a particle P.

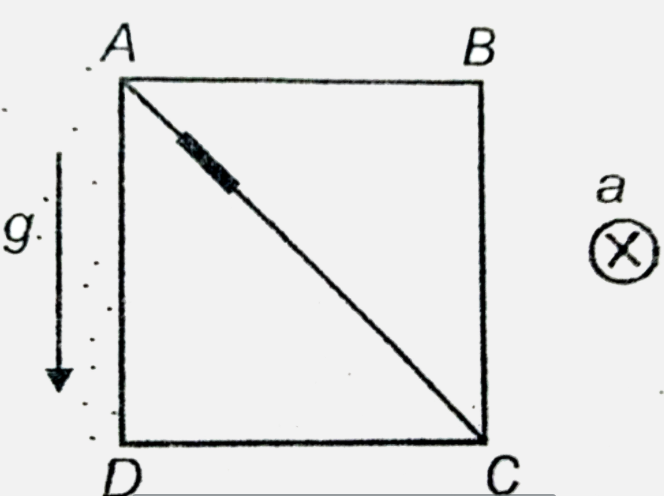
View SolutionA rectangular wire frame ABCD is in vertical plane is moving with a constant acceleration a into the plane as shown . Direction of gravity is shown inn figure . A collar can move on wire AC of length l . Coefficient of friction between wire and collar is μ. Find
 ltbr>
(i) The .....
(i) maximum acceleration a so that collar does not slip on wire.
ltbr>
(i) The .....
(i) maximum acceleration a so that collar does not slip on wire.
(ii) The time taken by collar to reach C if acceleration is half the value calculated in part
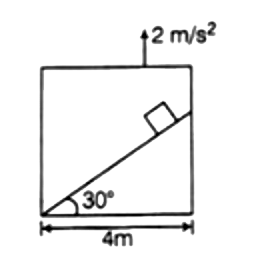
View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be
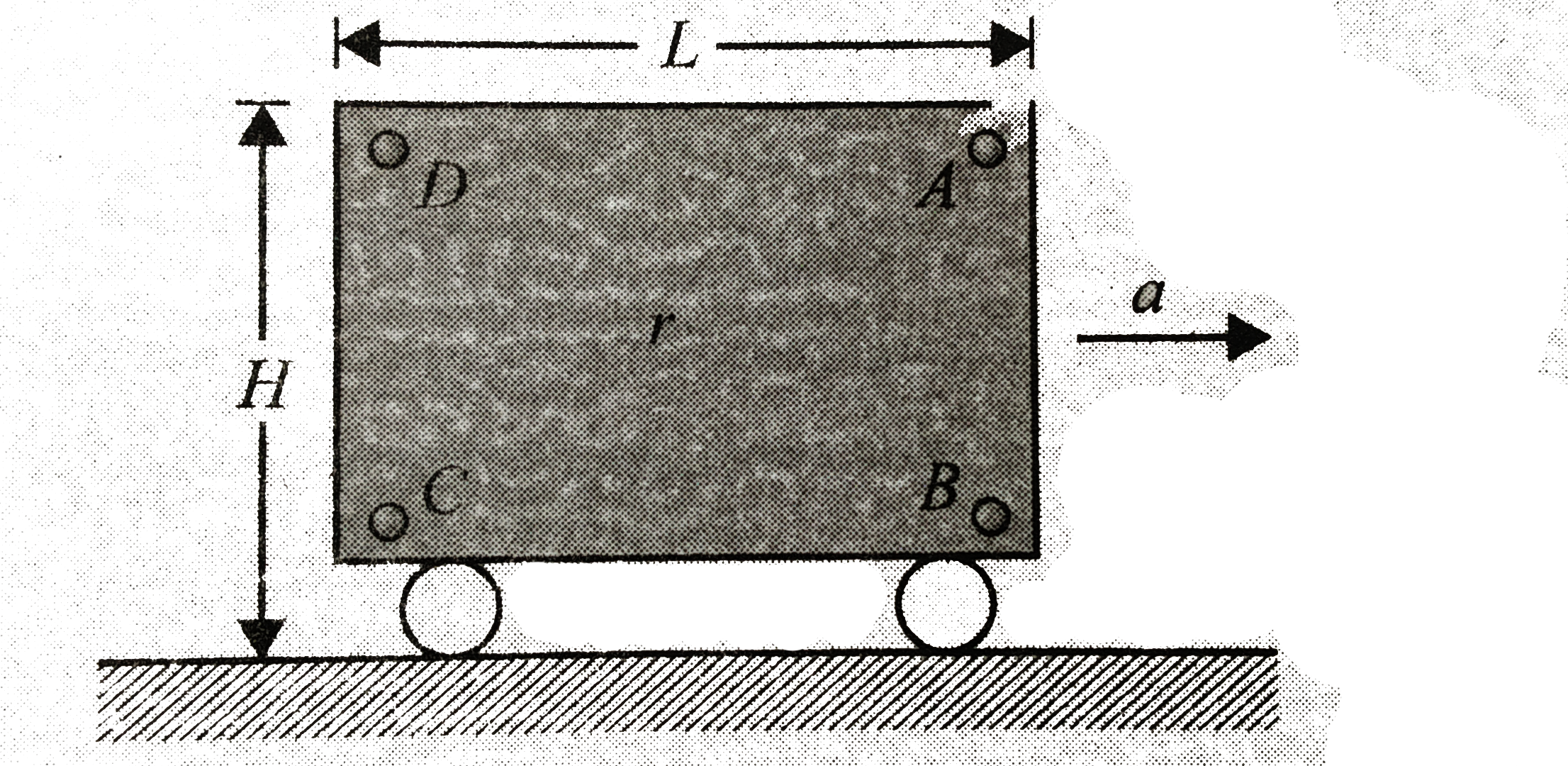
View SolutionA rectangular box is completely filled with a liquid of density ρ, as shown in Fig. The box is accelerated horizontally with a constant acceleration a. Determine the gauge pressures at the four points A,B,C and D.
View SolutionAn earth satellite is revolving in a circular orbit of radius a with velocity υ0. A gun in the satellite is aimed directly towards the earth. A bullet is fired from the gun with muzzle velocity υ02. Neglecting resistance offered by cosmic dust and recoil of gun, calculate maximum and minimum distance of bullet from the center of earth during its subsequent motion.
View SolutionA container contains an incompressible and non - viscous liquid of density ρ and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .
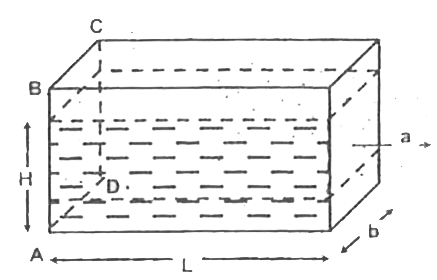
View SolutionInside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle θ with the vertical, when the particle will have maximum velocity with respect to the block is
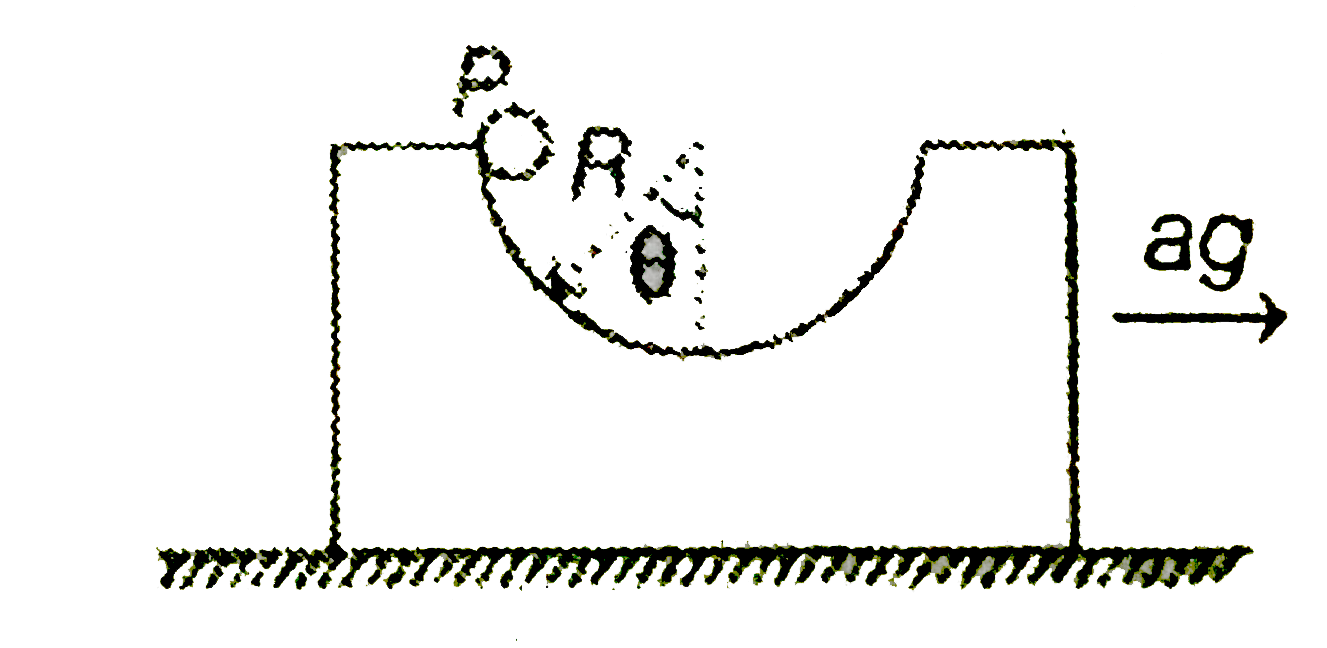
View SolutionA particle tide to the end of a string oscillates along a circular arc in a vertical plane. The other end of the string is fixed at the center of the circle. If the string has a breaking strength of twice the weight of the particles,
a. find the maximum distance that the particle can cover in one cycle of oscillation. The length of the string is 50cm.
b. Find the tension in the extreme position.
c. Find the acceleration of the particle at bottom and extreme position.
View Solution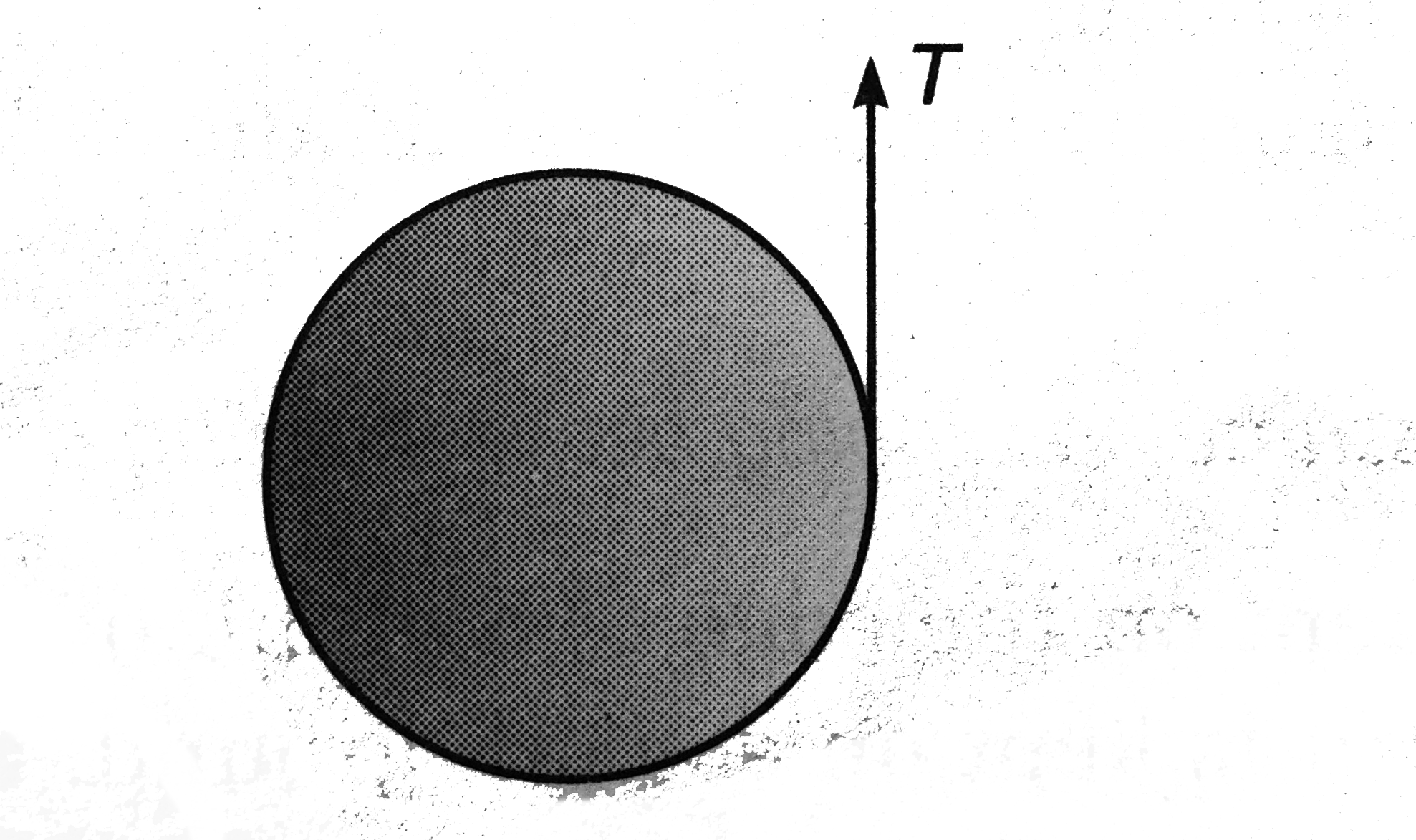
A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude a=2g3
(b). Find the tension in the string.
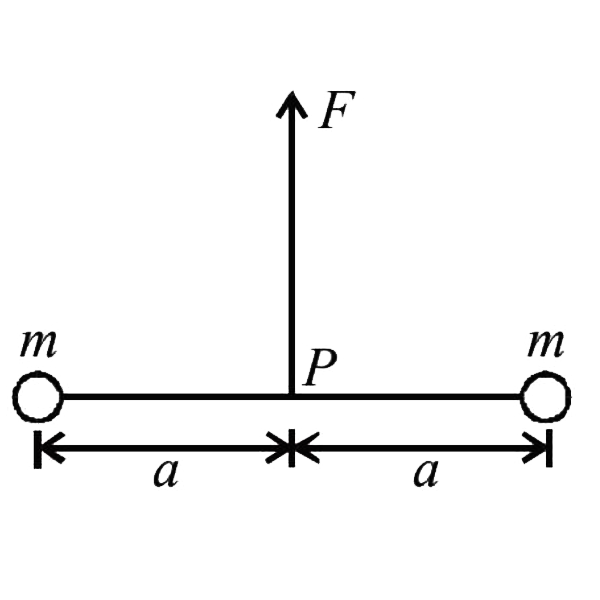
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
View Solution
